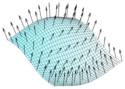
Normalvektor

En normalvektor är en vektor vars riktning är ortogonal (vinkelrät) mot ett annat objekt, till exempel en annan vektor eller geometriska objekt som linjer och ytor^[1]. Termen normal användes först inom tvådimensionell euklidisk geometri och avsåg linjer som är vinkelräta mot varandra, men en normal kan definieras för ett godtyckligt antal dimensioner.

En m-dimensionell vektor i en m-dimensionell rymd som är ortogonal mot samtliga vektorer i ett n-dimensionellt plan är en normalvektor till planet.

För ytor bestämda av en funktion, existerar för varje punkt i vilken den beskrivande funktionen är deriverbar, ett tangentrum, bestående av alla vektorer som tangerar ytan i punkten. Normalvektorerna till ytan är de vektorer som är ortogonala mot tangentrummen.

Normalvektorer är användbara för att projicera en punkt på ett plan och för att spegla en punkt i ett plan.

Beräkning av normalvektorer

Om en yta är given i implicit form som

${\displaystyle f(x,y,z)=0}$,

då ges en normalvektor i punkten (x, y, z) till ytan av gradienten

${\displaystyle \nabla f(x,y,z)}$

Om således f definierar ett tredimensionellt plan enligt

${\displaystyle f(x,y,z)=ax+by+cz+d=0}$

är en normalvektor till planet

${\displaystyle \nabla f(x,y,z)={\begin{bmatrix}a\\b\\c\\\end{bmatrix}}}$

I ett kartesiskt koordinatsystem kan en normalvektor till två tredimensionella vektorer u och v beräknas som vektorernas kryssprodukt:

${\displaystyle \mathbf {u} \times \mathbf {v} ={\begin{bmatrix}u_{2}\cdot v_{3}-u_{3}\cdot v_{2}\\u_{3}\cdot v_{1}-u_{1}\cdot v_{3}\\u_{1}\cdot v_{2}-u_{2}\cdot v_{1}\end{bmatrix}}}$

Referenser

Linjär algebra Grundläggande begrepp Skalär · Vektor · Noll · Ortogonalitet · Ekvationssystem · Rum · Linjärkombination · Inre produkt · Oberoende · Bas · Radrum · Kolonnrum · Nollrum · Gram-Schimdt · Egenvärde · Hölje · Linjäritet Vektoralgebra Kryssprodukt · Trippelprodukt Matriser Elementär · Block · Enhet · Determinant · Norm · Rang · Transformation · Rotation · Invers · Cramers regel · Trappstegsform · Spår · Transponat · Gausselimination · Symmetri · Addition Multilinjär algebra Geometrisk algebra · Yttre algebra · Bivektor · Multivektor · Tensor Konstruktioner Delrum · Dualrum · Funktionsrum · Kvotrum · Tensorprodukt Numerik Flyttal · Gles matris Kategori