Transponat

Inom linjär algebra är transponatet av en matris A en matris betecknad A^T. A^T kan beräknas på flera ekvivalenta sätt:

• Låt A:s rader bilda A^T:s kolonner.
• Låt A:s kolonner bilda A^T:s rader.
• Bilda A^T genom att reflektera A:s element i huvuddiagonalen.

Om a_ij är elementet på rad i, kolonn j i A ges elementen i A^T av:

${\displaystyle a_{ij}^{T}=a_{ji}}$.

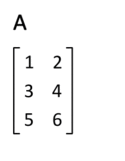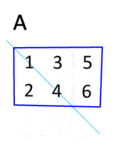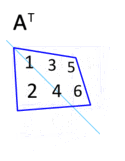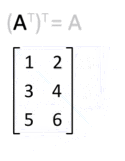
Exempel

${\displaystyle {\begin{pmatrix}1&2&1\\3&5&7\\9&7&3\end{pmatrix}}^{T}={\begin{pmatrix}1&3&9\\2&5&7\\1&7&3\end{pmatrix}}}$

${\displaystyle {\begin{pmatrix}1&7&5\\2&3&0\end{pmatrix}}^{T}={\begin{pmatrix}1&2\\7&3\\5&0\end{pmatrix}}}$

Egenskaper

Om A och B är matriser och c en skalär, så har man följande egenskaper:

• Transponatet är en involution:

${\displaystyle (A^{T})^{T}=A\,}$

• Transponatet är en linjär avbildning:

${\displaystyle (A+B)^{T}=A^{T}+B^{T}\,}$

${\displaystyle (cA)^{T}=cA^{T}\,}$

• Vid transponering av en produkt av matriser vänder man på ordningen:

${\displaystyle (AB)^{T}=B^{T}A^{T}\,}$

• Determinanten är invariant för transponering:

${\displaystyle \det(A^{T})=\det A\,}$

• Om ${\displaystyle A}$ är inverterbar är transponatet av inversen lika med inversen av transponatet:

${\displaystyle (A^{T})^{-1}=(A^{-1})^{T}\,}$

• Om ${\displaystyle A}$ endast har reella tal som element är ${\displaystyle A^{T}A}$ en positivt semidefinit matris.

Speciella matriser

Om D är en diagonalmatris är D^T = D.

En symmetrisk matris är en matris där

${\displaystyle A=A^{T}\,.}$

En skevsymmetrisk matris är en matris där

${\displaystyle A=-A^{T}\,.}$.

En ortogonal matris är en matris vars transponat är dess invers:

${\displaystyle A^{T}A=AA^{T}=I\,}$

${\displaystyle A^{T}=A^{-1}\,.}$

Se även

• Hermiteskt konjugat

Linjär algebra Grundläggande begrepp Skalär · Vektor · Noll · Ortogonalitet · Ekvationssystem · Rum · Linjärkombination · Inre produkt · Oberoende · Bas · Radrum · Kolonnrum · Nollrum · Gram-Schimdt · Egenvärde · Hölje · Linjäritet Vektoralgebra Kryssprodukt · Trippelprodukt Matriser Elementär · Block · Enhet · Determinant · Norm · Rang · Transformation · Rotation · Invers · Cramers regel · Trappstegsform · Spår · Transponat · Gausselimination · Symmetri · Addition Multilinjär algebra Geometrisk algebra · Yttre algebra · Bivektor · Multivektor · Tensor Konstruktioner Delrum · Dualrum · Funktionsrum · Kvotrum · Tensorprodukt Numerik Flyttal · Gles matris Kategori