Thomaes funktion

Thomaes function, Riemannfunktionen eller i engelsktalande länder popcornfunktionen är en funktion som är kontinuerlig i alla irrationella punkter och diskontinuerlig i alla rationella.[1]
Funktionen definition är
- , där och är heltal och bråket är förkortat så mycket som möjligt.
Kontinuitet i irrationella punkter
Låt vara ett irrationellt tal och för ett heltal. Vi kan definiera
- .
är alltså det kortaste avståndet till ett rationellt tal med nämnare högst . Då är
- om .
Detta visar att är kontinuerlig i .
Diskontinuitet i rationella punkter
Om finns det för varje ett (irrationellt) så att
- men .
Detta visar att är diskontinuerlig i .
Se även
Referenser
Externa länkar
 Wikimedia Commons har media som rör Thomaes funktion.
Wikimedia Commons har media som rör Thomaes funktion.
Media som används på denna webbplats
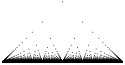
Plot of Thomae's function on the interval (0,1). Shown are all rational points with denominator at most 200. The topmost point in the middle shows f(1/2) = 1/2
Created using the following Java code:
public class Thomae {
static int gcd(int a, int b) {
while(a>0 && b>0) {
if(a>b) a -= a/b*b;
else b -= b/a*a;
}
return a>0 ? a : b;
}
public static void main(String[] args) {
int max = 200;
int width = 1280;
int height = 660;
int border = 20;
int x0 = border;
int x1 = width - border;
double dx = x1-x0;
int y0 = height - border;
double dy = -dx;
int r=5;
System.out.println("<?xml version=\"1.0\" standalone=\"no\"?>");
System.out.println("<!DOCTYPE svg PUBLIC \"-//W3C//DTD SVG 1.1//EN\" \"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd\">");
System.out.println("<svg width=\""+ width +"\" height=\""+ height +"\" xmlns=\"http://www.w3.org/2000/svg\" version=\"1.1\">");
for(int q=1; q<max; q++) for(int p=0; p<q; p++) if(gcd(p, q) == 1) {
System.out.println(" <circle cx=\""+ (x0+dx*p/q) + "\" cy=\""+ (y0+dy*1/q) +"\" r=\""+ r +"\" fill=\"black\" stroke=\"none\" />");
}
System.out.println("</svg>");
}
}