Singulär punkt

Den här artikeln behöver källhänvisningar för att kunna verifieras. (2023-07) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan.

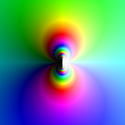
Singulär punkt, eller singularitet, är ett begrepp inom komplex analys. En singulär punkt är en punkt där en för övrigt analytisk funktion ${\displaystyle f}$ ej är definierad.

Man skiljer på tre olika sorters isolerade singulariteter (Låt ${\displaystyle f}$ vara analytisk i en omgivning av ${\displaystyle z_{0}}$, undantaget ${\displaystyle z_{0}}$):

• Hävbar singularitet: En punkt ${\displaystyle z_{0}}$ sägs vara en hävbar singularitet till f om ${\displaystyle |f(z)|}$ är begränsad i en punkterad omgivning kring ${\displaystyle z_{0}}$. I detta fall kan ${\displaystyle f}$ definieras i ${\displaystyle z_{0}}$ och på så vis ge en funktion analytisk i en omgivning av ${\displaystyle z_{0}}$ (medtaget ${\displaystyle z_{0}}$).
• Pol: En punkt ${\displaystyle z_{0}}$ sägs vara en pol till ${\displaystyle f}$ om ${\displaystyle \lim _{z\to z_{0}}|f(z)|=+\infty }$. I detta fall existerar en analytisk funktion ${\displaystyle g}$ (definierad i en omgivning kring ${\displaystyle z_{0}}$) och ett naturligt tal ${\displaystyle n}$ sådana att

${\displaystyle f(z)={\frac {g(z)}{(z-z_{0})^{n}}}.}$

• Väsentlig singularitet: En punkt ${\displaystyle z_{0}}$ sägs vara en väsentlig singularitet till ${\displaystyle f}$ om ${\displaystyle f(z_{0})}$ ej är definierad och ${\displaystyle z_{0}}$ varken är en hävbar singularitet eller en pol.

Se även

• Residy