Sfäriska koordinater

Sfäriskt koordinatsystem med den konvention med avseende på θ och φ som är vanligast inom matematiken

Sfäriska koordinater används i en form av tredimensionella koordinatsystem för att bestämma en punkts position med ett avstånd och två vinklar. Koordinaterna betecknas vanligen med r, φ och θ där

• r ≥ 0 är avståndet från origo till punkten. Detta avstånd kallas även för radie.

• 0 ≤ φ ≤ π är vinkeln mellan den positiva z-axeln och linjen från origo till punkten. Denna vinkel kallas ofta kolatitud eller polvinkel.

• 0 ≤ θ < 2π är vinkeln mellan den positiva x-axeln och en linje genom origo och projektionen av punkten på xy-planet. Denna vinkel kallas ofta longitud.

Omvandlingen från kartesiska till sfäriska koordinater sker genom

${\displaystyle r={\sqrt {x^{2}+y^{2}+z^{2}}}}$

${\displaystyle \varphi ={\mbox{arccos}}\,{\frac {z}{r}}}$

${\displaystyle \theta ={\mbox{arctan}}\,{\frac {y}{x}}}$

och omvandlingen från sfäriska koordinater till kartesiska görs enligt

${\displaystyle x=r\,\sin \varphi \,\cos \theta }$

${\displaystyle y=r\,\sin \varphi \,\sin \theta }$

${\displaystyle z=r\,\cos \varphi }$

Inom fysiken är beteckningarna ofta de motsatta, så att θ är kolatitud och φ longitud.

Tillämpningar

Det frekvensberoende strålningsmönstret för en högtalare visat med hjälp av sfäriska koordinater för sex olika frekvenser

Sfäriska koordinater används inom astronomi, rymdfart, geografi, navigation och andra vetenskaper och områden som innefattar positions- och riktningsbestämningar på jorden, i solsystemet eller i universum. Härvid används exempelvis ekvatoriella koordinater (med ekvatorsplanet som basplan), ekliptiska koordinater (med ekliptikan som basplan) och horisontella koordinater (med horisontalplanet som basplan). Dessa system använder elevation (vinkeln mot basplanet, det vill säga 90°-φ) i stället för polvinkel/kolatitud. Elevationen kallas även latitud (dock ej geodetisk latitud, vilken är lodlinjens vinkel mot ekvatorialplanet), deklination eller altitud, medan θ kallas longitud, rektascension, timvinkel eller azimut. För elevationen, ε, gäller:

${\displaystyle \varepsilon ={\mbox{arcsin}}\,{\frac {z}{r}}}$

och

${\displaystyle x=r\,\cos \varepsilon \,\cos \theta }$

${\displaystyle y=r\,\cos \varepsilon \,\sin \theta }$

${\displaystyle z=r\,\sin \varepsilon }$

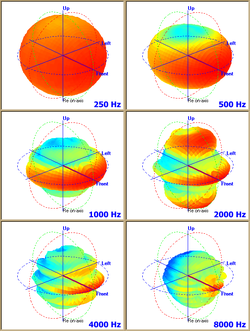
Tredimensionell modellering av högtalare används för att förutsäga högtalarnas beteenden. Ett antal sfäriska grafer över ett stort frekvensområde behövs då strålningsegenskaperna är starkt beroende av frekvensen. Sfäriska grafer visar åskådligt hur en högtalare tenderar att bli rundstrålande vid låga frekvenser.

Sfäriska koordinatsystem är också vanliga för utveckling av 3D-spel, till exempel för att rotera "kameran" kring spelarens position.

Generaliserade sfäriska koordinater

Sfäriska koordinater kan generaliseras till n dimensioner:

${\displaystyle {\begin{aligned}x_{1}&=r\cos(\phi _{1})\\x_{2}&=r\sin(\phi _{1})\cos(\phi _{2})\\x_{3}&=r\sin(\phi _{1})\sin(\phi _{2})\cos(\phi _{3})\\&{}\,\,\,\vdots \\x_{n-1}&=r\sin(\phi _{1})\cdots \sin(\phi _{n-2})\cos(\phi _{n-1})\\x_{n}&=r\sin(\phi _{1})\cdots \sin(\phi _{n-2})\sin(\phi _{n-1})\end{aligned}}}$

Vinklarna kan beräknas från

${\displaystyle {\begin{aligned}\tan(\phi _{n-1})&={\frac {x_{n}}{x_{n-1}}}\\\tan(\phi _{n-2})&={\frac {\sqrt {{x_{n}}^{2}+{x_{n-1}}^{2}}}{x_{n-2}}}\\&{}\,\,\,\vdots \\\tan(\phi _{1})&={\frac {\sqrt {{x_{n}}^{2}+{x_{n-1}}^{2}+\cdots +{x_{2}}^{2}}}{x_{1}}}\end{aligned}}}$

Genom omnumrering erhålls ett rekursivt schema för koordinaterna:

${\displaystyle {\begin{aligned}x_{n}&=r\cos(\phi _{n-1})\\x_{n-1}&=r\sin(\phi _{n-1})\cos(\phi _{n-2})\\x_{n-2}&=r\sin(\phi _{n-1})\sin(\phi _{n-2})\cos(\phi _{n-3})\\&{}\,\,\,\vdots \\x_{2}&=r\sin(\phi _{n-1})\cdots \sin(\phi _{2})\cos(\phi _{1})\\x_{1}&=r\sin(\phi _{n-1})\cdots \sin(\phi _{2})\sin(\phi _{1})\end{aligned}}}$

Vinklarna kan då beräknas genom

${\displaystyle ||{\vec {L}}_{k}||=\operatorname {sgn}(x_{k}){\sqrt {x_{k}^{2}+||{\vec {L}}_{k-1}||^{2}}}={\frac {x_{k}}{||x_{k}||}}{\sqrt {x_{k}^{2}+||{\vec {L}}_{k-1}||^{2}}}}$

och med ${\displaystyle ||{\vec {L}}_{0}||=0}$ erhålls

${\displaystyle \tan(\phi _{k})={\frac {\sqrt {x_{k}^{2}+||{\vec {L}}_{k-1}||^{2}}}{x_{k+1}}}={\frac {||{\vec {L}}_{k}||}{x_{k+1}}}}$

och där längdkoordinaten är

${\displaystyle r=||{\vec {L}}_{n}||}$

Exempel

För n = 3 och med de gemensamma koordinataxlarna x, y, z gäller

${\displaystyle {\begin{aligned}x_{3}&=z=r\cos(\phi _{2})\\x_{2}&=x=r\sin(\phi _{2})\cos(\phi _{1})\\x_{1}&=y=r\sin(\phi _{2})\sin(\phi _{1})\\\end{aligned}}}$

För vinklarna gäller då

${\displaystyle {\begin{aligned}\tan(\phi _{2})={\frac {||{\vec {L}}_{2}||}{x_{3}}}&={\frac {\sqrt {x_{2}^{2}+x_{1}^{2}}}{x_{3}}}={\frac {\sqrt {x^{2}+y^{2}}}{z}}\\\tan(\phi _{1})={\frac {||{\vec {L}}_{1}||}{x_{2}}}&={\frac {\sqrt {x_{1}^{2}}}{x_{2}}}={\frac {y}{x}}\end{aligned}}}$

Externa länkar

• Wikimedia Commons har media som rör Sfäriska koordinater.
  Bilder & media