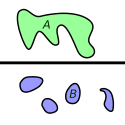
Sammanhängande rum

Illustration över en sammanhängande mängd A och en osammanhängande mängd B.

Ett sammanhängande rum är inom matematiken ett topologiskt rum som intuitivt "hänger ihop". Matematiskt innebär detta att rummet inte kan uttryckas som en union av två disjunkta öppna mängder. Ett starkare begrepp är ett bågvis sammanhängande rum där alla par av punkter kan förbindas med en kurva.

En delmängd till ett topologiskt rum sägs vara en sammanhängande mängd om den är sammanhängande sett som ett underrum till det ursprungliga rummet.

Sammanhängande rum

Ett sammanhängande rum definieras vanligtvis som ett topologiskt rum som inte är unionen av två disjunkta öppna mängder, men det finns flera ekvivalenta villkor som lika gärna kan användas som definition för begreppet. Låt X vara ett topologiskt rum, då följande villkor är ekvivalenta med att X är sammanhängande:

• X kan inte skrivas som en union av två disjunkta slutna mängder.
• De enda mängderna i X som är både öppna och slutna är den tomma mängden och X.
• De enda mängderna i X med tom rand är den tomma mängden och X.
• Varje kontinuerlig funktion från X till en diskret mängd bestående av åtminstone två element är en konstant funktion.

Sammanhängande mängder kan karakteriseras med att D som en delmängd till ett topologiskt rum X är sammanhängande om och endast om det inte existerar två icke-tomma delmängder A och B till X sådana att ${\displaystyle D=A\cup B}$ och ${\displaystyle ({\overline {A}}\cap B)\cup (A\cap {\overline {B}})=\varnothing }$.

Sammanhängande komponenter

En sammanhängande komponent till en punkt x i ett topologiskt rum X är unionen av alla sammanhängande underrum till X som innehåller x. En sammanhängande mängd är en sammanhängande komponent om och endast om den inte är en äkta delmängd till någon annan sammanhängande mängd i rummet.

De sammanhängande komponenterna till ett rum kan också konstrueras genom ekvivalensrelationen x ~ y om och endast om det finns ett sammanhängande underrum som innehåller både x och y, då de sammanhängande komponenterna är ekvivalensklasserna som uppstår.

De sammanhängande komponenterna bildar en partition av det ursprungliga rummet. Om ett topologiskt rum är sammanhängande har det bara en sammanhängande komponent.

Bågvis sammanhängande rum

Denna mängd (färgad) är bågvis sammanhängande. Komplementet (vit) är inte bågvis sammanhängande eftersom det inte går att dra en kurva från de små "öarna" till resten av mängden utan att gå utanför den. Den färgade mängden är inte enkelt sammanhängande, för en kurva som går på ena sidan om en av "öarna" kan inte kontinuerligt deformeras till en som går på andra sidan ön.

Ett topologiskt rum X är bågvis sammanhängande om det för varje par av punkter x och y finns en kontinuerlig kurva

${\displaystyle \gamma :[a,b]\to X}$

sådan att ${\displaystyle \gamma (a)=x}$ och ${\displaystyle \gamma (b)=y}$.

Bågvis sammanhängande komponenter

Som för vanliga sammanhängande komponenter kan man definiera de bågvis sammanhängande komponenterna till ett topologiskt rum som ekvivalensklasserna som uppstår under ekvivalensrelationen x ~ y om och endast om det finns en kurva mellan x och y.

De bågvis sammanhängande komponenterna bildar även de en partition av det ursprungliga topologiska rummet.

Enkelt sammanhängande rum

Ett topologiskt rum X är enkelt sammanhängande om varje kontinuerlig kurva som förenar ett par av punkter x och y går att kontinuerligt deformera till varje annan kontinuerlig kurva som förenar samma två punkter.

Lokalt sammanhängande rum

Ett topologiskt rum X är lokalt sammanhängande vid x om det finns en sammanhängande omgivning till x. Om X är lokalt sammanhängande vid alla av sina punkter sägs X vara ett lokalt sammanhängande rum.

Ett topologiskt rum X är lokalt sammanhängande om och endast om det för alla öppna mängder U i X är så att varje sammanhängande komponent av U är öppen i X.

Exempel

• De reella talen R och intervall och strålar i R är sammanhängande.
• Unionen av intervallen ${\displaystyle [0,1[}$ och ${\displaystyle ]1,2]}$ utrustad med underrumstopologin är osammanhängande.
• Konvexa mängder är sammanhängande, till och med enkelt sammanhängande.
• R utan nollan är osammanhängande. R² utan origo är sammanhängande, men inte enkelt sammanhängande. R³ utan origo är enkelt sammanhängande.
• Topologiska vektorrum över sammanhängande kroppar är sammanhängande.
• Den allmänna linjära gruppen ${\displaystyle \operatorname {GL} (n,\mathbb {R} )}$ är inte sammanhängande; den består av de två komponenterna bestående av matriser med positiv respektive negativ determinant. Dock är ${\displaystyle \operatorname {GL} (n,\mathbb {C} )}$ sammanhängande.

Egenskaper

• Sammanhängande och bågvis sammanhängande mängder och rum bevaras av kontinuerliga avbildningar.
• Varje bågvis sammanhängande rum är sammanhängande.
• Varje kvotrum av ett (bågvis) sammanhängande rum är (bågvis) sammanhängande.
• Varje produktrum en familj av (bågvis) sammanhängande rum är (bågvis) sammanhängande.
• Alla sammanhängande komponenter är slutna, men i regel inte öppna.
• De sammanhängande komponenterna i lokalt sammanhängande rum är alltid öppna.
• Bågvist sammanhängande komponenter behöver vara varken öppna eller slutna.

Referenser

• Munkres, James (2000). Topology. Prentice Hall. ISBN 0-13-181629-2 
• Hocking, John; Gail Young (1988). Topology. Dover Publications. ISBN 0-486-65676-4 
• Lang, Serge (1983). Real Analysis. Addison-Wesley. ISBN 0-201-14179-5