Rotationskropp
| Den här artikeln behöver källhänvisningar för att kunna verifieras. (2023-06) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan. |
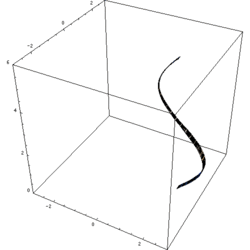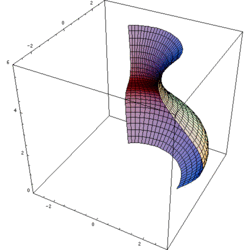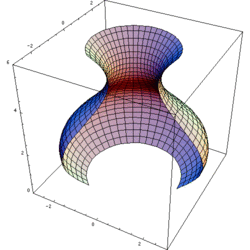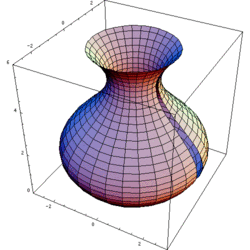
En rotationskropp är i matematiken den volym som innesluts av kurvan när den roterar kring en axel. Exempel på fysiska objekt som har formen av rotationskroppar är föremål som svarvats eller drejats, exempelvis en skål eller ett basebollträ.
Volymen av en rotationskropp beräknas som integralen av rotationskroppens snittyta från dess början till dess slut. Denna är lika med funktionsvärdet i kvadrat gånger pi (och motsvarar cirkelns area som funktion av dess radie).
Volymen av rotationskroppen av mellan a och b, roterad runt x-axeln, är alltså
Volymen av rotationskroppen av mellan a och b, roterad runt y-axeln, är

I teorin kan en rotationskropp som är oändligt lång ändå ha ändlig volym. (Fysiska rotationskroppar har dock alltid begränsad längd.)
Arean av rotationskroppen av mellan a och b, roterad runt x-axeln, är
Arean av rotationskroppen av mellan a och b, roterad runt y-axeln, är
Media som används på denna webbplats
Författare/Upphovsman: Tkgd2007, Licens: CC BY-SA 3.0
A new incarnation of Image:Question_book-3.svg, which was uploaded by user AzaToth. This file is available on the English version of Wikipedia under the filename en:Image:Question book-new.svg
Författare/Upphovsman: Macks, Licens: CC BY-SA 2.5
Representation of a rotation of a sine curve


