Rörströmning
Rörströmning är en del av strömningsmekaniken och hydrauliken som omfattar analys och beräkningar av hur vätskor strömmar i rör. Inom rörströmning analyseras bland annat sambandet mellan strömningshastighet och tryckfall samt olika strömningsmönster.
Rörströmning jämfört med kanalströmning
Mer specifikt handlar rörströmning om fullgående rör, som helt innesluter den strömmande vätskan. Ett närbesläktat område är kanalströmning, som omfattar strömning i kanaler och liknande fall, där det finns en fri vätskeyta. Ekvationerna som används vid strömningsberäkningar är olika vid rörströmning och kanalströmning på grund av förekomsten av en fri vätskeyta. Om en vätska strömmar i ett rör som inte är fullgående, det vill säga inte helt innesluter vätskan, så rör det sig om kanalströmning. Ett exempel på det sistnämnda är dagvattenbrunnar.
Jämfört med kanalströmning, så underlättas flödesberäkningarna vid rörströmning av att rörets inre tvärsnittsarea är helt oberoende av flödet. Dessutom är rören betydligt mer jämna i sin form jämfört med kanaler, öppna diken och naturliga vattendrag, vilket medger att strömningsförlusterna (inklusive eventuella tilläggsförluster) kan beräknas mer noggrant vid rörströmningen. Däremot blir energilinjens lutning betydligt knepigare att beräkna, då det per definition inte förekommer någon fri vattenyta inom rörströmningen.
Friktionsfri strömning
Om strömningen sker friktionsfritt, stationärt och inkompressibelt beskrivs flödet av Bernoullis ekvation. Friktionsfritt flöde innebär att vätskan kan strömma fritt förbi rörväggen utan att någon friktion uppstår och att vätskans viskositet inte spelar någon roll. Dessa villkor är inte uppfyllda vid verklig rörströmning. Det innebär att Bernoullis ekvation beskriver en idealiserad situation. Bernoullis ekvation kan trots detta användas för att beräkna sambandet mellan tryck, strömningshastighet och höjd för en strömmande vätska.
Bernoullis ekvation är uppkallad efter Daniel Bernoulli som publicerade sina resultat i Hydrodynamica 1738.[1] Effekterna av friktion på vätskors strömning var ej kända vid denna tid.
Strömning med friktion
I verkliga strömningsfall leder friktionen mellan vätskan och rörväggen till att strömningshastigheten exakt vid rörväggen alltid är noll. Detta kallas för vidhäftningsvillkoret (engelska: no-slip condition) och är en utgångspunkt i de ekvationer för rörströmning som tar hänsyn till friktionen.[2]
Eftersom strömninghastigheten är noll vid rörväggen, varierar strömningshastigheten över rörets tvärsnitt. I ett cirkulärt rör är hastigheten som högst i mitten av röret. Hur mycket strömningshastigheten varierar beror bland annat på vätskans viskositet, eftersom olika vätskeskikt måste glida över varandra, vilket ger upphov till friktionsförluster i samband med rörströmning.
Laminär och turbulent rörströmning
Vid låga strömningshastigheter sker strömningen laminärt. Vid högre strömningshastigheter sker strömningen turbulent. Laminär strömning sker strukturerat och ordnat, utan att flödeslinjerna korsar varandra. Turbulent strömning sker kaotiskt och ostrukturerat, och medför en omblandning i röret.
Friktionsförlusterna är större vid turbulent strömning än vid laminär strömning.
Beräkningar vid olika strömningstillstånd
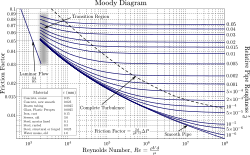
Det finns två huvudsakliga metoder att genomföra beräkningar av rörströmning vid olika värden på Reynolds tal. Den ena metoden är att använda Moody-diagrammet, som innehåller kurvor för alla olika strömningstillstånd i ett diagram. Den andra metoden är att identifiera det aktuella strömningstillståndet och använda rätt ekvation för just detta strömningstillstånd.
Översikt över olika rörströmingstillstånd och dess beräkningsmässiga följder
Utifrån Moody-diagrammet kan fem olika strömningstillstånd identifieras. För de flesta av dessa strömningstillstånd finns också olika ekvationer framtagna. Vid all flödesdimensionering är det alltså av yttersta vikt att korrekt kunna bedöma strömningstillståndet och därmed vilken flödes-ekvation som är tillämplig. Annars kan resultatet i värsta fall bli katastrofalt med stora översvämningar och syrgasbrist som följd.
| Strömningstillstånd | Strömningstyp | Undertyp | Tillämplig ekvation | Gränsvärden |
|---|---|---|---|---|
| Strömningstillstånd 1 | Laminär | - | Hagen-Poiseuilles lag | g1 |
| Övergångszon I | Växlande | - | Osäker zon | g1, g2 |
| Strömningstillstånd 2A | Turbulent | Hydraulisk glatt | Prandtl-Nikuradses formel | g2, g3, g′3 |
| Övergångszon II | Turbulent | Mellanting | Prandtl-Nikuradse-Colebrooks formel | g3, g4 |
| Strömningstillstånd 2B | Turbulent | Hydrauliskt rått | Nikuradse-Prandtls formel | g4, g′3 |
För alla ovanstående stömningstillstånd finns olika kritiska gränsvärden framtagna.
Andra viktiga ekvationer
Se även
- Dimensionerande flöde
- Dimensionerande flödestal
- Flödesdimensionering
- Flödesmätning
- Kanalströmning
- Strömningsmekanik
- Täckdike
Källor
- ^ ”Hydrodynamica”. Britannica Online Encyclopedia. http://www.britannica.com/EBchecked/topic/658890/Hydrodynamica#tab=active~checked%2Citems~checked&title=Hydrodynamica%20–%20Britannica%20Online%20Encyclopedia. Läst 30 oktober 2008.
- ^ KTH: Navier-Stokes ekvationer, läst 2019-04-28
Media som används på denna webbplats
Författare/Upphovsman:
- Original diagram: S Beck and R Collins, University of Sheffield (Donebythesecondlaw på engelska Wikipedia)
- Conversion to SVG: Marc.derumaux
Moody Diagram
Författare/Upphovsman: Joseasorrentino, Licens: CC BY-SA 3.0
Transition from laminar flow to turbulent flow