Portal:Matematik/Utvald artikel/Arkiv

2013

14 augusti –

I matematiska termer är hyperbolisk geometri en viss typ av icke-euklidisk geometri. Termen ”hyperbolisk geometri” introducerades av Felix Klein år 1871.

Två hyperboliska linjer definieras som parallella om dessa är disjunkta, vilket betyder att dessa inte har några gemensamma punkter.

Det femte axiomet i euklidisk geometri är parallellaxiomet och detta axiom är mycket omtalat i och med det inte är lika enkelt att formulera samt att innebörden inte är lika självklar. Euklides försökte bevisa parallellaxiomet ur de fyra första axiomen utan resultat.

► Läs mer

5 juli – 14 augusti

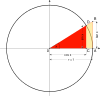
Trigonometri är läran om förhållandet mellan vinklar och sidor i en triangel. Trigonometrin har sina största praktiska, direkta tillämpningar inom lantmäteri och navigation där den används för triangulering, men används teoretiskt inom ett flertal områden inom matematiken, bland annat geometri och komplex analys och därmed även fysik.

► Läs mer

26 maj – 5 juli

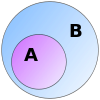
En mängd är en samling av objekt. De objekt som ingår i en mängd kallas mängdens element. I axiomatisk mängdteori, till exempel Zermelo-Fraenkels mängdteori, finns ett antal axiom som fastställer hur mängder får bildas. De får till exempel inte ha sig själva som element. Men i stort sett är det nästan inga begränsningar på vad en mängd får innehålla.

En mängd är ändlig eller oändlig beroende på om den innehåller ett ändligt eller oändligt antal element. Ändliga mängder kan anges genom att man räknar upp elementen inom klammrar; exempelvis {2, 3, 5, 7} är mängden av alla primtal under 10. Mängden av alla primtal är emellertid oändlig (det finns oändligt många primtal), så den kan man inte ange på detta sätt. Ett mer generellt sätt att ange mängder är genom att skriva {x : A(x)}, vilket betyder mängden av alla x som har egenskapen A (märk att andra tecken än kolon kan användas i litteraturen). Till exempel kan mängden av samtliga primtal skrivas {x : x är ett primtal}. Nästan alla matematiska begrepp som finns kan reduceras till mängder.

► Läs mer