Polyeder

En polyeder (av grekiskans polús, många, och hédra, yta) är en kropp som begränsas av ett ändligt antal plan och har ett antal månghörningar, polygoner, som sidoytor.
Med en regelbunden polyeder avser man normalt en polyeder där alla begränsningsytor är lika regelbundna polygoner och att samma antal sidor (eller kanter) möts i varje hörn. Det finns precis fem sådana konvexa polyedrar, vilket bevisades av Euklides. Dessa kallas platonska kroppar. En triangulär bipyramid (som fås genom sammansättning av två tetraedrar yta mot yta) är inte regelbunden trots att den är konvex och alla sidor är lika, eftersom tre sidor möts i två av hörnen och fyra sidor i de övriga.
Om man även tillåter att kanter och sidor skär varandra (de ställen där så sker är "falska" hörn eller kanter) finns fyra regelbundna polyedrar till, de så kallade Kepler–Poinsot-polyedrarna.[1]
De arkimediska kropparna har regelbundna månghörningar som begränsningsytor, men dessa behöver inte vara lika sinsemellan. Däremot är alla hörn lika. Det finns precis tretton arkimediska kroppar (femton om två "spegelbilder", enantiomorfer, räknas separat).
Ytterligare polyedrar som består av regelbundna polygoner är regelbundna prismor och regelbundna antiprismor samt de så kallade Johnsons kroppar.
Johnsons kroppar är polyedrar som inte är platonska, arkimediska, prismor eller antiprismor och har sidor som alla är regelbundna månghörningar. Man har visat att det finns 92 sådana polyedrar. En fyrsidig pyramid, med en kvadrat som bas och fyra liksidiga trianglar som sidoytor, är exempel på en sådan.
- Kuboktaedern har kvadrater och liksidiga trianglar som begränsningsytor. Den är en arkimedisk kropp
- En stjärntetraeder är ett exempel på en polyeder där alla begränsningsytorna är lika. Den är inte en platonsk kropp eftersom den inte är konvex
- En triangulär bipyramid är inte regelbunden eftersom hörnen inte är lika.
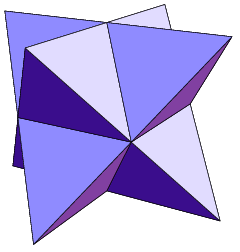
- Den "stora dodekaedern" är en av Kepler–Poinsot-polyedrarna. De "äkta" kanterna och hörnen är markerade i silver respektive guld. De tolv "äkta" sidorna är regelbundna femhörningar.[2]
Se även
Källor
- Weisstein, Eric W., "Polyhedron", MathWorld. (engelska)
- ^ Weisstein, Eric W., "Kepler-Poinsot Solid", MathWorld. (engelska)
- ^ Weisstein, Eric W., "Great Dodecahedron", MathWorld. (engelska)
Externa länkar
Media som används på denna webbplats
Simple picture of a Stella octangula / Star Tetrahedron
Författare/Upphovsman: The original uploader was Cyp på engelska Wikipedia., Licens: CC BY-SA 3.0
A Hexahedron (cube). A regular polyhedron.
Image d'un cuboctaèdre


![Den "stora dodekaedern" är en av Kepler–Poinsot-polyedrarna. De "äkta" kanterna och hörnen är markerade i silver respektive guld. De tolv "äkta" sidorna är regelbundna femhörningar.[2]](http://upload.wikimedia.org/wikipedia/commons/thumb/d/d2/Great_dodecahedron.png/283px-Great_dodecahedron.png)




