Pascals triangel

Den här artikeln behöver källhänvisningar för att kunna verifieras. (2023-06) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan.

Inom matematiken är Pascals triangel en geometrisk framställning av binomialkoefficienterna i form av en triangel. Den namnges ofta efter matematikern och fysikern Blaise Pascal, men var känd utanför Europa långt före Pascals levnad.

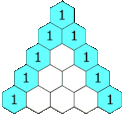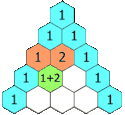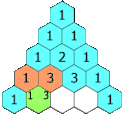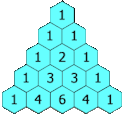
Något förenklat är varje rad ett element längre än föregående rad och varje elements värde är summan av elementen ovanför till vänster och höger (om dessa existerar). På så sätt har varje rad en etta i början och slutet. Rad- och kolumnräkningen börjar båda på noll.

Således, det fjärde elementet på rad fem beräknas genom att det tredje och fjärde elementet på föregående rad adderas.

Triangeln kan ses som en tillämpning av Pascals identitet

${\displaystyle {n \choose k}={n-1 \choose k-1}+{n-1 \choose k}}$

där ${\displaystyle n,\,k\geq 0}$ och ${\displaystyle n\geq k}$ med initialvärdet ${\displaystyle {n \choose 0}={n \choose n}=1}$

Således motsvarar första elementet i triangeln binomialkoefficienten ${\displaystyle {0 \choose 0}}$ och kan alltså refereras till som rad ${\displaystyle (n+1)}$.

Talen i mittkolumnen kallas centrala binomialkoefficienter.

Bevis

${\displaystyle {n-1 \choose k-1}+{n-1 \choose k}=}$

${\displaystyle ={\frac {(n-1)\ldots [(n-1)-(k-1)+1]}{(k-1)!}}+{\frac {(n-1)\ldots [(n-1)-k+1]}{(k)!}}=}$

${\displaystyle =(n-1)(n-2)\ldots (n-k+1)\left({\frac {1}{(k-1)!}}+{\frac {n-k}{k!}}\right)=}$

${\displaystyle =(n-1)(n-2)\ldots (n-k+1)\cdot {\frac {k+n-k}{k!}}=}$

${\displaystyle ={\frac {n(n-1)(n-2)\ldots (n-k+1)}{k!}}={n \choose k}}$

Tillämpningar av Pascals triangel

Den n:te potensen av ett binom, ${\displaystyle (a+b)^{n}\quad }$, kan utvecklas med hjälp av binomialsatsen och Pascals triangel enligt följande:

Rad 0								1							(x - y)0 = 1
Rad 1							1		1						(x - y)1 = x - y
Rad 2						1		2		1					(x - y)2 = x2 - 2xy + y2
Rad 3					1		3		3		1				(x - y)3 = x3 - 3x2y + 3xy2 - y3
Rad 4				1		4		6		4		1			(x - y)4 = x4 - 4x3y + 6x2y2 - 4xy3 + y4
Osv.

Se även

• binomialsatsen