Oskulerande kurva

Inom differentialgeometrin är en oskulerande kurva (oskulerande, vidrörande, från latin osculatio, kyssande, osculum, kyss^[1][2]) en plan kurva från en given kurvfamilj som i en viss punkt, oskulationspunkten, ansluter sig så nära som möjligt till en annan given kurva, d.v.s. har samma värde och så många derivator gemensamma med denna givna kurva som möjligt. Om den oskulerande kurvan har k derivator gemensamma med den givna kurvan sägs den ha kontakt^[3] eller oskulera av ordning k.

Exempel

• Tangenten till en kurva i en given punkt är den oskulerande kurvan i punkten från familjen räta linjer. Den har förstaderivatan gemensam med kurvan, d.v.s. kontakt av ordning ett.
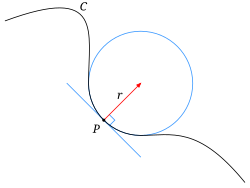
• Den oskulerande cirkeln, eller krökningscirkeln, till en punkt på en kurva, d.v.s. den oskulerande kurvan från familjen cirklar, har första- och andraderivatorna gemensamma med kurvan i punkten, d.v.s. kontakt av ordning två.
• Den oskulerande parabeln till en kurva har första, andra och tredje derivatorna gemensamma med kurvan - kontakt av ordning tre.
• Det oskulerande kägelsnittet har de fyra första derivatorna gemensamma med kurvan i oskulationspunkten - kontakt av ordning fyra.

Källor

• Philip Franklin, 1925, Osculating Curves and Surfaces
• Thomas Jehpson, 1826, The Fluxional Calculus, kap XI, sid 392 ff.
• Oskulera i Nordisk familjebok, Uggleupplagan.

Referenser