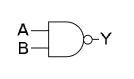
NAND
| Logisk operator (Logisk grind) |
|---|
|
| Se även |
NAND, not-AND, är en logisk operator, en logisk funktion som är negation av logisk konjunktion. Med hjälp av satsvariablerna p och q och satslogiska konnektiv, kan p NAND q skrivas
Tillsammans med NOR är NAND, som betecknas med symbolen | (Sheffers streck) de enda dyadiska operatorerna, vilka var och en kan uttrycka alla de andra satslogiska konnektiven. Detta utnyttjades tidigare vid så kallad NAND-logik vid konstruktionen av digitala kretsar.
Representation
Operatorn betecknas med symbolen | eller med "NAND". Med satslogiska beteckningar är p | q:
Sanningsfunktion och sanningstabell
NAND beskrivs i satslogiken som en funktion – en sanningsfunktion – av de ingående påståendenas sanningsvärden och funktionsvärdena ges i en sanningstabell, där S = sann och F = falsk och jämförs här med konjunktion):
| p | q | p NAND q | p AND q |
| F | F | S | F |
| F | S | S | F |
| S | F | S | F |
| S | S | F | S |
Tekniska lösningar
I elektriska kretsar, pneumatik, hydraulik, mekanik etcetera, kan funktioner som motsvarar NAND realiseras.
Parallellkoppling
Om två brytare kopplas parallellt på nedanstående sätt, måste en eller båda brytarna vara i läge 0 för att lampan ska vara tänd. Detta motsvarar funktionen NAND.
NAND-grind
NAND-grinden är tillsammans med NOR-grinden de enda enskilda logiska funktioner med två ingångar, som förmår realisera alla andra logiska funktioner. Alltså, kan man (teoretiskt) bygga varje krets genom endast kombinera lämpliga NAND-grindar, även om bygget oftast blir smidigare om man använder de grindar som är speciellt anpassade till det aktuella bygget.
|
Källor
- Karl-Johan Bäckström, Diskret matematik, Studentlitteratur, Lund 1984.
- Per-Erik Danielsson, Digital teknik, Studentlitteratur, Lund 1974.