Monty Hall-problemet

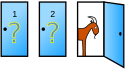
Monty Hall-problemet är ett spelteoretiskt problem som bygger på sannolikheter. Det är löst baserat på det amerikanska spelet "Let's make a deal". Namnet kommer från spelets presentatör, Monty Hall. I spelet får spelaren se tre stängda dörrar - bakom en finns en bil, och bakom de två andra finns getter. Spelet börjar med att spelaren får välja en dörr, utan att öppna den. Därefter öppnar presentatören, som vet vad som finns bakom dörrarna, en av de två resterande dörrarna (men aldrig den med bilen) och visar att denna dörr inte innehåller vinsten. Spelaren får då ytterligare ett val, nämligen att antingen byta dörr eller hålla fast vid sitt första val.^[1]

Frågeställningen är om chanserna att vinna ökar om spelaren byter dörr.

Problemet kallas ibland Monty Hall-paradoxen då den korrekta lösningen motsäger ett intuitivt resonemang om sannolikheterna för att göra rätt val.

Problemet kan formuleras så här: I spelet får spelaren se tre dörrar – bakom en finns en bil, och bakom de två andra finns en get. Spelet börjar med att spelaren väljer en dörr, utan att öppna den. Därefter öppnar presentatören, som vet vad som finns bakom dörrarna, en av de två resterande dörrarna och visar att denna dörr inte innehåller vinsten. Presentatören ger därefter spelaren ytterligare ett val, nämligen att byta dörr.

I denna, den vanligaste, varianten måste presentatören öppna en dörr med en get och presentatören måste också erbjuda spelaren möjligheten att byta efter det att dörren med geten har öppnats.

Ja, det är till spelarens fördel att ändra sitt val. Chansen att vinna dubbleras av att man ändrar sitt val jämfört med att hålla fast vid originalvalet.

Lösningen kan visualiseras genom att visa att det finns tre olika scenarion, samtliga med 1/3 sannolikhet:

• Spelaren väljer bilen. Spelledaren presenterar get A eller get B. Byte ger förlust. (Alternativ 1 nedan.)
• Spelaren väljer get A. Spelledaren presenterar get B. Byte ger vinst. (Alternativ 2 nedan.)
• Spelaren väljer get B. Spelledaren presenterar get A. Byte ger vinst. (Alternativ 3 nedan.)

Som synes är det bara om man valde rätt dörr till att börja med som det kan bli fel om man byter. Då det är 1/3 chans att man valde rätt dörr från början blir det också bara 1/3 chans att man förlorar om man byter, och således 2/3 chans att bytet ger vinst.

1. Presentatören visar en av getterna Spelaren väljer bilen (sannolikhet 1/3) Byte resulterar i en av getterna 2. Presentatören måste visa get B Spelaren väljer get A (sannolikhet 1/3) Byte ger vinst 3. Presentatören måste visa get A Spelaren väljer get B (sannolikhet 1/3) Byte ger vinst

Spelaren har lika stor chans att initialt välja bilen, get A eller get B. Byte ger vinst i 2/3 av fallen.

Ett sätt att troliggöra för den skeptiske att det är bättre att byta är att föreställa sig 100 olika dörrar, 99 getter och 1 bil. Sen när man gjort sitt val så öppnar spelledaren 98 av de andra dörrarna med getter bakom. Det finns då bara 2 dörrar kvar. Ska jag stå fast vid min första chansning eller byta? Det är ju då bara 1 på 100 att pricka rätt på direkten. Vid andra valet är det bara 2 dörrar kvar och fortfarande 1 på 100 att man råkade träffa rätt i första valet. Precis som i fallet ovan är det då (n-1)/n d.v.s. 99/100 att vinna om man byter.

Den lösning som beskrivs ovan gäller under de förutsättningar som anges i avsnittet. Andra varianter ger andra sannolikheter och andra lösningar för vad som, för spelaren, är det bästa valet. Om förutsättningarna ändras, till exempel genom att spelledaren kan välja att inte erbjuda spelaren att byta, är beräkningen annorlunda. Flera diskussioner om Monty Hall-problemets rätta lösning har orsakats av att debattörerna har använt olika varianter av problemet utan att vara medvetna om det.

En generalisering av problemet är att använda n antal dörrar. I det första steget väljer man då en dörr, varefter spelledaren öppnar en dörr med en get bakom. Man får sedan valet att stå fast vid sitt val eller byta. Detta fortsätter tills det bara är två oöppnade dörrar kvar. Frågeställningen är huruvida, och i så fall, hur många gånger, man bör byta dörr, och när?

Den bästa strategin är att hålla fast vid sitt val ända tills på slutet, då man byter.^[2] Med denna stategi är sannolikheten att vinna (n-1)/n, vilket bevisades av Bapeswara Rao och Rao.^[3][4]

Istället för att enbart räkna på sannolikheter kan man analysera problemet uttryckt i informationsteori. Spelledaren sitter från början på all information och spelaren har ingen information (om var bilen befinner sig). Säg att det finns fyra dörrar så behövs två bitar information för att ange vilken dörr som bilen finns bakom. Om spelledaren öppnar två av de fyra dörrarna så det bara finns två dörrar kvar, då behövs plötsligt bara en bit information för att säga bakom vilken av dörrarna som bilen står. Spelledaren har alltså gett deltagaren information om var bilen finns.

Craig F. Whitaker formulerade problemet i en insändare till Marilyn vos Savants kolumn i Parade Magazine 1990.^[5] Denna formulering blev berömd då hennes svar orsakade stor kontrovers.

Formuleringen var enligt resonemanget ovan: Antag att du är med i en tv-lek där du får välja mellan tre dörrar. Bakom en dörr finns en bil, bakom de andra två, getter. Du väljer dörr 1, och tv-värden, som vet vad som finns bakom alla dörrar, öppnar en annan dörr, säg nummer 3, vilken visar en get. Han frågar därefter: "Vill du byta till dörr nummer 2?". Är det då till din fördel att ändra ditt val?

… och svaret blev ett entydigt JA!.

Som ett exempel på hur höga diskussionens vågor gick kan följande exempel ges från synpunkterna som kom in från läsarkretsen:

"You blew it, and you blew it big! Since you seem to have difficulty grasping the basic principle at work here, I'll explain. After the host reveals a goat, you now have a one-in-two chance of being correct. Whether you change your selection or not, the odds are the same. There is enough mathematical illiteracy in this country, and we don't need the world's highest IQ propagating more. Shame!"
– Scott Smith, Ph.D. University of Florida^[5]

• Wikimedia Commons har media som rör Monty Hall-problemet.
  Bilder & media