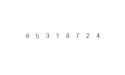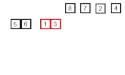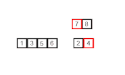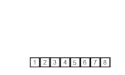Merge sort

Den här artikeln behöver källhänvisningar för att kunna verifieras. (2023-07) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan.

Merge sort

Parvis jämförelse, stabil sorteringsalgoritm

Under­klass till	• algoritm  • kombinatorisk algoritm   • sorteringsalgoritm
Upp­täc­ka­re eller upp­fin­na­re	John von Neumann
Upp­täckts­da­tum	1945
Tids­komp­lex­i­tet i värsta fall	${\displaystyle O(n\log n)}$
Tids­komp­lex­i­tet i bästa fall	${\displaystyle O(n\log n)}$
Tids­komp­lex­i­tet i medel	${\displaystyle O(n\log n)}$
Rums­komp­lex­i­tet i värsta fall	${\displaystyle O(n)}$
Best-case space comp­lex­i­ty	${\displaystyle O(1)}$

Merge Sort är en stabil sorteringsalgoritm. Den sorterar n objekt med tidskomplexitet O (n log n) i värsta fall. Att algoritmen är stabil betyder att element med lika värde (exempelvis 7 och 7) hamnar i samma ordning i utdata som de var i indata.

Merge Sort-algoritmen är av typen söndra och härska, och har konceptuellt följande steg för att sortera en lista med storlek n:

1. Dela upp listan i n lika stora dellistor (alla med längd 1)
2. Slå samman dellistorna parvis i sorterad ordning
3. Upprepa steg två, tills det bara finns en lista kvar

Den slutgiltiga listan är original-listan i sorterad ordning.

Algoritmen har en tidskomplexitet på O(n log n) i värsta fall, vilket är snabbare än exempelvis Quicksort som har en värsta-fallet-tid på O(n²). Nackdelen med Mergesort är utrymmesbehovet då en ny kopia av listan måste skapas för att kunna genomföra alla sammanslagningar. Det innebär att utrymmeskomplexiteten är O(n), jämfört med exempelvis Quicksort vilken klarar sig på O(log n).^[1]

Implementering

Nedan följer en rekursiv implementering i Python:

def MergeSort( lista ):
  if len( lista ) == 1:
    return lista

  #Dela listan i två delar
  mitten = len(lista)//2
  lista_1 = MergeSort( lista[0:mitten] )
  lista_2 = MergeSort( lista[mitten:] )

  #Slå samman de sorterade listorna (härska)
  retur_lista = []
  while len( lista_1 ) > 0 and len( lista_2 ) > 0:
    if lista_1[0] < lista_2[0]:
      retur_lista.append( lista_1[0] )
      lista_1.pop(0)
    else:
      retur_lista.append( lista_2[0] )
      lista_2.pop(0)

  #Lägg till de element som "blev över" i slutet
  retur_lista += lista_1
  retur_lista += lista_2
  return retur_lista

Referenser