Maximum likelihood-metoden

Maximum likelihood-metoden, ofta förkortat ML-metoden även kallad maximimetoden, är en objektiv metod inom statistiken för att hitta skattningar för parametrar i en sannolikhetsfördelning som beskriver en samling data. Metoden skattar parametern genom att välja det värde på parametern som maximerar sannolikheten av de observerade värdena.[1]
Bakgrund
Ibland kan det vara vanskligt att hitta parametrarna för en sannolikhetsfördelning genom att granska en serie utfall. Ett exempel kan vara om man experimentellt ska uppskatta turtätheten för en (helt punktlig) busslinje genom att göra en serie mätningar för hur länge man får vänta på bussen (en stokastisk variabel med rektangulärfördelning). Om de uppmätta väntetiderna är 2, 3, 5 och 14 minuter så blir medelvärdet 6 minuter. Den skattade turtätheten blir i så fall 12 minuter, vilket är orimligt. Den slutsatsen indikerar att man behöver granska sitt val av statistisk modell.
Likelihood-funktionen

Vid användning av ML-metoden använder man den så kallade likelihood-funktionen för ett slumpmässigt stickprov x1, x2, ..., xn från en fördelning beroende av en okänd parameter :
eller, om data () är utfall av oberoende variabler:[2]
där f är fördelningens täthetsfunktion om fördelningen är kontinuerlig och fördelningens sannolikhetsfunktion om fördelningen är diskret.
Det värde där antar sitt största värde kallas för ML-skattningen av .
Egenskaper
Maximum likelihood-metoden har följande egenskaper:
- Skattningen behöver inte vara väntevärdesriktig.[3][4]
- Metoden är invariant för monotona funktioner.[5][4] Man maximerar ofta logaritmen av likelihoodfunktionen.
- Skattningen behöver inte vara konsistent.[3] En konsistent skattnings fel och varians går mot noll om sampelstorleken går mot oändligheten.[6]
- Om det finns en tillräcklig estimator T, kommer maximum likelihood-metoden att finna en lösning beroende på T.[7]
- Om det finns en väntevärdesriktig effektiv estimator, kommer maximum likelihood-metoden att hitta den.[3][7]
- Skattningen behöver inte vara unik.[8]
- Skattningen behöver inte ens finnas. Det förekommer ofta när parametern är definierad på ett öppet eller halvöppet intervall.[9]
- När sampelstorleken ökar, går skattningen mot att bli normalfördelad.[3]Den uppnår asymptotiskt Cramér-Rao-gränsen(en). Det betyder att dess varians är inversen av Fisherinformationen(en).[7]
Referenser
Noter
- ^ Blom, Gunnar; Björn Holmquist (1998). Statistikteori med tillämpningar. Studentlitteratur. sid. 62-64. ISBN 91-44-00323-4
- ^ Blom, Gunnar; Jan Enger, Gunnar Englund, Jan Grandell, Lars Holst (2005). Sannolikhetsteori och statistikteori med tillämpningar. Studentlitteratur. sid. 254. ISBN 978-91-44-02442-4
- ^ [a b c d] Råde 1963, s. 185.
- ^ [a b] Kiefer 1987, s. 202.
- ^ Råde 1963, s. 184.
- ^ Lindgren 1968, s. 270.
- ^ [a b c] Lindgren 1968, s. 284.
- ^ Kiefer 1987, s. 200.
- ^ Kiefer 1987, s. 204.
Källor
- Kiefer, Jack; Gary Lorden (1987). Introduction to Statistical Inference. New York: Springer. ISBN 0-387-96420-7
- Lindgren, Bernard W. (1968). Statistical theory. New York: Macmillan
- Råde, Lennart (1963). Sannolikhetslära och statistik. Stockholm: Biblioteksförlaget
Externa länkar
 Wikimedia Commons har media som rör Maximum likelihood-metoden.
Wikimedia Commons har media som rör Maximum likelihood-metoden.
Media som används på denna webbplats
Författare/Upphovsman: Lfiondella, Licens: CC BY 3.0
Plot of the maximum likelihood estimate of the Goel-Okumoto model, shown with the observed failure data.
Författare/Upphovsman: HilberTraum, Licens: CC BY-SA 3.0
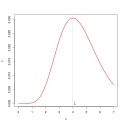
Likelihood function for Poisson model with observations x1 = 3, x2 = 5