Maple

Maple
Utvecklare	Maplesoft
Först släppt	1982
Senaste utgåva	2021 (10 mars 2021)
Skriven i	C, Java, Maple
Operativsystem	multi-plattform
Plattform	Windows (7, 8 och 10), macOS, Linux
Typ	datoralgebrasystem
Språk	Engelska, m. fl.[1]
Webbplats	http://www.maplesoft.com/products/maple/

Maple är ett datoralgebrasystem, det vill säga ett datorprogram för symbolisk lösning av matematiska problem och tekniska beräkningar, från företaget Maplesoft. Maple utvecklades 1981 vid Symbolic Computation Group - University of Waterloo i Ontario, Kanada. Maple täcker aspekter av teknisk databehandling, inklusive visualisering, dataanalys, matrisberäkning och anslutning. En verktygslåda, MapleSim, lägger till funktionalitet för multidomain fysisk modellering och kodgenerering.

Användningsområden

• Matematiska beräkningar: symbolisk och numerisk lösning av matematiska problem t. ex. ekvationer, integraler och "pretty-printing" av matematiska formler

• Differentialekvation, Ordinär differentialekvation, Partiell differentialekvation

• Elementär och speciell funktionsbibliotek

• Finansiell modellering, analys och applikationsutveckling

• Flervariabelanalys

• Grafisk framställning

• Komplexa tal och komplex analys

• Linjär algebra: Singulärvärdesuppdelning

• Matrisoperationer och matrisalgebra

• Optimeringslära, Linjärprogrammering

• Statistik och dataanalys: Regressionsanalys, Hypotesprövning, ANOVA, Principalkomponentanalys

• Test och uppmätning: Hårdvarukoppling och dataanalys för test och mätapplikationer

• Teknisk beräkning: analys, signalprocesser, visualisering och algoritmutveckling

• Tidsserieanalys

Anslutningar

• Matlab anslutningar ^[2]

• Excel add-in ^[3]

• Kodgenerering för C, C#, Fortran, Java, Javascript, Julia, Matlab, Perl, Python, R, VB

• Gränssnitt till CAD, HTTP, SQL, .NET

Exempel

Procedur

myfac := proc(n::nonnegint)
  local out, i;
  out := 1;
  for i from 2 to n do
      out := out * i
  end do;
  out
end proc;

Funktion

myfac := n -> product( i, i=1..n );

Integration

${\displaystyle \int \cos \left({\frac {x}{a}}\right)dx}$.

int(cos(x/a), x);

Resultat:

${\displaystyle a\sin \left({\frac {x}{a}}\right)}$

Determinant

M:= Matrix([[1,2,3], [a,b,c], [x,y,z]]);

${\displaystyle {\begin{bmatrix}1&2&3\\a&b&c\\x&y&z\end{bmatrix}}}$

LinearAlgebra:-Determinant(M);

Resultat:

${\displaystyle bz-cy+3ay-2az+2xc-3xb}$

Serie expansion

series(tanh(x),x=0,15)

Resultat:

${\displaystyle x-{\frac {1}{3}}\,x^{3}+{\frac {2}{15}}\,x^{5}-{\frac {17}{315}}\,x^{7}}$

${\displaystyle +{\frac {62}{2835}}\,x^{9}-{\frac {1382}{155925}}\,x^{11}+{\frac {21844}{6081075}}\,x^{13}+O(x^{15})}$

Lös ekvation numeriskt

f := x^53-88*x^5-3*x-5 = 0
fsolve(f)

Resultat:

-1.097486315, -.5226535640, 1.099074017

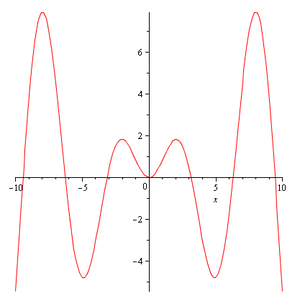
Visualisering av en enkel variabel funktion

plot(x*sin(x),x=-10..10);

Visualisering av en funktion av två variabler

plot3d(2-x-(y^2-x^2)^0.5), x=0..1, y=0..1);

Animation

${\displaystyle f:=2\cdot k^{2}/\cosh(k\cdot (x-4\cdot k^{2}\cdot t))^{2}}$

plots:-animate(subs(k = .5, f), x=-30..30, t=-10..10, numpoints=200, frames=50, color=red, thickness=3);

2D bell solution

plots:-animate3d(cos(t*x)*sin(3*t*y), x=-Pi..Pi, y=-Pi..Pi, t=1..2);

3D animation of function

M := Matrix([[400,400,200], [100,100,-400], [1,1,1]], datatype=float[8]):
plot3d(1, x=0..2*Pi, y=0..Pi, axes=none, coords=spherical, viewpoint=[path=M]);

Maple plot3D fly-through

Laplace transform

f := (1+A*t+B*t^2)*exp(c*t);

${\displaystyle (1+A\cdot t+B\cdot t^{2})\cdot e^{c\cdot t}}$

inttrans:-laplace(f, t, s);

Resultat:

${\displaystyle {\frac {1}{s-c}}+{\frac {A}{(s-c)^{2}}}+{\frac {2B}{(s-c)^{3}}}}$

inttrans:-invlaplace(1/(s-a),s,x)

Resultat:

${\displaystyle e^{ax}}$

Fourier transform

inttrans:-fourier(sin(x),x,w)

Resultat:

${\displaystyle \mathrm {I} \pi \,(\mathrm {Dirac} (w+1)-\mathrm {Dirac} (w-1))}$

Se även

• Mathcad
• Mathematica
• MATLAB
• GNU Maxima

Referenser

Noter

Externa länkar

• (engelska) Maplesoft
• (engelska) Produktdokumentation
• (engelska) MapleSim
• (danska) Maple til danske gymnasier