Klotoid

En klotoidkurva.

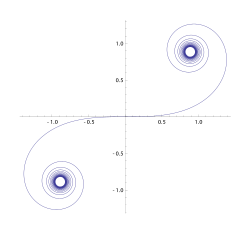
Klotoid är en kurva vars krökning varierar linjärt med dess längd. Klotoider används ofta för att ge mjuka övergångar mellan raksträckor och kurvor på vägar och järnvägar, men används även i till exempel berg- och dalbanor, bland annat på Gröna Lund och Liseberg.[1]

Utseende

Rent geometriskt är klotoiden en typ av spiral.

I CAD-system finns ofta inbyggda funktioner för att skapa klotoidövergångar i en linje mellan ett antal kurvor.

Historia

På tidiga järnvägar rullade tågen sakta, vilket gjorde att det inte behövdes mjuka övergångar mellan raksträckor och kurvbågar. Mot slutet av 1800-talet ökade hastigheterna och därmed ökade slitaget på räls och vagnshjul på avsnitt där kurvradien var snäv. Därmed kom insikten att det behövs mjuka övergångar med gradvis ökande krökning, det vill säga ett spiralformat element, mellan raksträcka och kurvbåge. Rankine[2] citerar flera sådana kurvor. Klotoiden fick alltså på sent 1800-tal en viktig tillämpning inom järnvägsbyggande. Äran för att ha formulerat den första exakta beskrivningen av klotoidens ekvation brukar bland järnvägsfackfolk tillskrivas Ellis Holbrook.[3]

Klotoiden, eller den likvinkliga spiralen, har dock en mycket längre historia än inte bara järnvägen utan till och med hela vetenskapen om matematik. Spiraler har skapats sedan urhistorisk tid, bland annat i form av arrangemanget av solrosfrön i solrosor och hos snäckskal, bland många andra naturfenomen. Klotoiden är känd under många olika namn. Descartes gav den år 1638 namnet "likvinklig spiral". Torricelli (död 1647) visade att radierna ändras gradvis och att vinklarna ökar med jämn takt. Från detta härledde han ekvationen s = a*r. Jacob Bernoulli (1654–1705), kallade klotoiden "logaritmisk spiral" och var så fascinerad av det matematiska elementets skönhet att han begärde att den benämningen skulle stå på hans gravsten. Några andra vanligt förekommande benämningar är Euler-integral, Eulers spiral, Fresnel-integral samt Cornus spiral.

Användning

Klotoider används ofta i järnvägssammanhang. Se spårgeometri. Klotoiden ger en övergångskurva mellan rakspår och cirkulärkurvan och därefter åter en övergångskurva mot nästa rakspår. Klotoider kan även gälla vertikala kurvor (lutningar) och rälsförhöjningar (sidolutningar). Klotoidkrökningen gör att påkänningarna mellan hjul och räls minskar, vilket ökar livslängden både räls och hjul. Därtill kan klotoider minska risken för rörelsesjuka. Det kan också vara en linjär krökningsändring mellan två olika stora cirkulära kurvor. På moderna spårvägar bygger man nästan uteslutande med övergångskurvor i trafikspår då många moderna vagnkonstruktioner är känsliga för plötsliga ändringar i kurvradier.

Klotoider används också som övergångskurvor på vägar, eftersom den linjära krökningsförändringen hos klotoiden motsvarar en jämn rattrörelse hos ett fordon som framförs i konstant hastighet, och medför att vägen då följer fordonets naturliga bana in i och ut ur kurvan. På vägar är trafiken dock inte spårbunden på samma sätt som spårtrafik och därför kan bilförare ofta välja ett bekvämt körspår i övergång mellan raklinje och kurva även utan övergångskurvor, men det kräver att vägen är relativt bred så att föraren kan ta ut svängen utan att lämna körfältet.

Relation till vägtrafiksäkerhet

En vägkurvas utformning har stor påverkan på vägtrafiksäkerheten, en väl utformad kurva ska vara konsekvent, lätt att överblicka och vara "förlåtande" i den meningen att ett förarmisstag ska gå att rätta till utan att leda till svåra konsekvenser.[4] Användning av övergångskurvor leder generellt till en jämnare hastighet och en mindre ryckig färd (rattrörelserna behöver inte vara lika snabba), men om övergångskurvan är för lång kan det bli svårt för föraren att avgöra hur skarp kurvan till slut kommer att bli och risken är då att föraren kommer med för hög hastighet.[5] Övergångskurvor kan också leda till att kurvan blir något snävare än vad den annars hade varit, vilket i sin tur ökar risken för olyckor.

Klotoider kan förutom i övergångskurvor också användas i så kallade ägglinjekurvor. En ägglinjekurva är en sammansatt kurva med minst två olika radier och klotoiden kan då användas för att få en mjuk övergång mellan de båda radierna.[6][7] Djupstudier av dödsolyckor på landsväg i Norge visar att dåliga egenskaper hos vägen bidragit till nästan hälften av dödsolyckorna. De norska studierna pekar på att den enskilt farligaste vägfaktorn är väglinjeföring som kan "lura" fordonsförare; drygt hälften av vägrelaterade olyckor hamnar i denna grupp. Efter sammanställning av djupstudierna, lyfter Statens Vegvesen särskilt fram ägglinjekurvor som allvarligt bidragande faktor bakom många olyckor.[8] Även Statens Havarikommisjon for Transport har identifierat varierande kurvradie som en svår vägomständighet vid allvarliga trafikolyckor.[9]

Naturlig förekomst

Klotoider förekommer i många sammanhang i naturen. På snäckskal, hos växter och i rymden.

Klotoider hos snäckor i gruppen Prosobranchia; bild av Ernst Haeckel

När man böjer ett material, till exempel ett sågblad, bildas i vissa fall klotoidövergångar eftersom de ger minst energi i böjningen. Detta gäller till exempel om materialet är fast inspänt i ena änden.[10]

Se även

Referenser

  1. ^ Pendrill, Ann-Marie (2005). ”Fysik och liv”. Fysikaktuellt (Svenska Fysikersamfundet) (nr 2): sid. sid 3. http://www.fysikersamfundet.se/wp-content/uploads/2005_2.pdf. Läst 19 januari 2018. 
  2. ^ Rankine, William (1883). A Manual of Civil Engineering (17th edition ed.). Charles Griffin. pp. 651–653
  3. ^ Charles Crandall, Railroad Gazette, 3 Dec 1880
  4. ^ Anonymous (17 oktober 2016). ”Getting initial safety design principles right” (på engelska). Mobility and transport - European Commission. https://ec.europa.eu/transport/road_safety/specialist/knowledge/road/getting_initial_safety_design_principles_right_en. Läst 28 december 2020. 
  5. ^ Stewart & Chudworth. "A Remedy for Accidents at Bends". Traffic Eng & Control. Vol 31. No 2.
  6. ^ Vägars och gators utformning begrepp och grundvärden.. Trafikverket. 2012. ISBN 978-91-7467-396-8. OCLC 940051783. https://www.worldcat.org/oclc/940051783. Läst 28 december 2020 
  7. ^ Espen, Strandvik Haugvik (2018). Risikokurver - analyse av utforkjøringsrisikofaktorer på 2-feltsveger. sid. 10. https://vegvesen.brage.unit.no/vegvesen-xmlui/handle/11250/2614570. Läst 28 december 2020 
  8. ^ Dybdeanalyse av dödsulykker i vegtrafikken i Region Midt i 2006. Årsrapport fra ulykkesanalysegruppe. Statens Vegvesen, Norge
  9. ^ ”Rapport om møteulykke på E6 i Bjørnbærvika i Mo i Rana 1. desember 2016, SHT Rapport VEI 2017/05”. Arkiverad från originalet den 22 januari 2018. https://web.archive.org/web/20180122125038/https://www.aibn.no/Veitrafikk/Avgitte-rapporter/2017-05. Läst 21 januari 2018. 
  10. ^ ”Böjning”. Omkrets arkitektur. juli 2007. Arkiverad från originalet den 16 oktober 2008. https://web.archive.org/web/20081016055515/http://www.omkrets.se/bending/index.htm. Läst 17 mars 2010. 

Externa länkar

Media som används på denna webbplats

Clothoid curve.svg
Författare/Upphovsman: D.328 2008/11/4 10:38 (UTC), Licens: CC BY-SA 3.0
Clothoid curve, a type of transition curve.
Haeckel Prosobranchia.jpg
  1. Calcar triumphans (Philippi) = Guildfordia triumphans (Philippi, 1841), from above
  2. Conus imperialis (Linné) = Conus imperialis Linnaeus, 1758[1]
  3. Harpa ventricosa (Lamarck) = Harpa Röding Röding, 1798[2]
  4. Murex tenuispinus (Lamarck) = Murex pecten pecten Lightfoot, 1786[3]
  5. Murex inflatus (Lamarck) = Chicoreus ramosus (Linnaeus, 1758)[4]
  6. Fusus longicauda (Lamarck) = Fusinus colus (Linnaeus, 1758)[5], cut open
  7. Astralium imperiale (Chemnitz) = Astraea heliotropium Martyn, 1784, from below
  8. Astralium imperiale (Chemnitz) = Astraea heliotropium Martyn, 1784, from above Astraea heliotropium