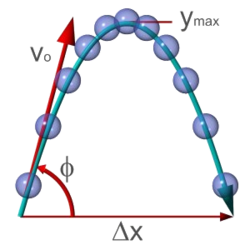
Kastparabel

Den här artikeln behöver källhänvisningar för att kunna verifieras. (2018-06) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan.

Kastparabel.

Studsande boll fotograferad med stroboskopisk blixt, 25 bilder per sekund.

En kastparabel är den bana som ett föremål som kastas beskriver då föremålet endast påverkas av tyngdaccelerationen i ett gravitationsfält och där hastigheten i horisontalled är större än noll. Föremålets hastighet i vertikalled skall inte vara större än att tyngdaccelerationen till riktning och storlek kan anses vara konstant under kastet. Även om start och landningspunkt ligger på olika höjd kommer föremålets bana att bli en del av en parabel om luftmotståndet försummas.

Summan av rörelseenergin och lägesenergin är konstant om ingen hänsyn tas till luftmotståndet. Hastighetens storlek vid början och slutet av luftfärden är densamma, vid plant underlag och ideala förhållanden.

Om ett föremål släpps eller kastas kommer det vid havsnivå i Sverige att utsättas för en konstant acceleration g av cirka 9,82 m/s² riktad mot jordens centrum, oavsett vilken hastighet och riktning föremålet har.

Accelerationen är tidsderivatan av hastigheten så hastigheten i vertikalled är

${\displaystyle v_{y}\ =v_{y0}-gt}$

där ${\displaystyle \ v_{y0}}$ är den vertikala utgångshastigheten.

Hastigheten är tidsderivatan av positionen så höjden blir

${\displaystyle h\ =h_{0}+v_{y0}t-{\frac {gt^{2}}{2}}}$

där ${\displaystyle \ h_{0}}$ är utgångshöjden. Eftersom föremålet antas ha konstant hastighet i horisontalled kommer termen med t ²-faktorn att ge den typiska parabelformen.

Om föremålet kastas med utgångshastigheten ${\displaystyle v_{0}}$ och vinkeln ${\displaystyle \phi }$ i förhållande till horisontalplanet blir den vertikala utgångshastigheten ${\displaystyle v_{y0}=v_{0}\sin \phi }$ medan den horisontella hastigheten blir ${\displaystyle v_{x0}=v_{0}\cos \phi .}$

Luftmotståndet beror på den ögonblickliga totalhastigheten i förhållande till luften, alltså vektorsumman av horisontal- och vertikalkomposanterna och kan appoximativt anses vara proportionellt mot kvadraten av vektorsummans belopp.

Kastbanor i luft

En projektilbana i luft skiljer sig från beskrivningen ovan. Genom luftmotståndet kommer projektilens hastighet att bromsas varför banans högsta punkt kommer att vara närmare nerslagspunkten. Nerslagsvinkeln kommer att vara större än utgångsvinkeln φ. Den största kastvidden erhålls vid 45° utgångsvinkel i ett lufttomt rum, men vid en mindre vinkel i luft. För gevär nås den längsta skottvidden vid ca 35°.

Projektilbanor för olika utgångsvinklar

Se även

• ballistik