Königsbergs sju broar
Königsbergs sju broar är ett klassiskt matematiskt problem inom grafteori och topologi. Den schweiziske matematikern Leonhard Euler visade i artikeln Solutio problematis ad geometriam situs pertinentis år 1736[1] att problemet var olösligt, vilket bidrog till grafteorins uppkomst.
Bakgrund
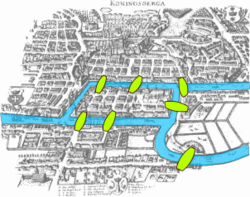
Under 1700-talet var staden Königsberg (nuvarande Kaliningrad) i dåvarande Ostpreussen uppdelad i fyra delar: den norra och södra stranden av floden Pregel som flöt genom staden, samt två öar mitt i floden – en mindre västlig och en större östlig. Den mindre av öarna, Kneiphof, var stadens centrum, där bland annat katedralen låg. Från denna ö gick två broar till den norra stranden och två broar till den södra stranden, samt en bro till den större ön, från vilken det i sin tur gick en bro till den norra stranden och en bro till den södra stranden. Totalt var därmed öarna och fastlandet förbundna med varandra genom sju broar. Det sades att stadens invånare på sina söndagspromenader försökte hitta ett sätt att gå genom staden på ett sådant sätt att de passerade varje bro endast en gång. Ingen hade dock lyckats med detta.
Problemets lösning
Den schweiziske matematikern Leonhard Euler fick höra talas om problemet med Königsbergs sju broar och beslöt sig för att lösa det. Problemet var alltså att finna en promenadväg som passerar varje bro exakt en gång. År 1736 visade han att det inte finns någon lösning på problemet; det går inte att göra en sådan promenad. För att lösa problemet formulerade Euler om det som ett problem beträffande en abstrakt graf med följande utseende:

I denna graf motsvarar prickarna (noderna) positioner på någon av öarna eller fastlandet, och linjerna (kanterna) broar. Euler visade att
- om det finns fler än två noder som har ett udda antal förbindelser så finns det ingen lösning.
Beviset räcker för att lösa problemet med Königsbergs broar, vare sig det krävs att start- och slutpunkten sammanfaller eller inte:
Om en punkt har ett udda antal förbindelser måste den vara antingen start- eller slutpunkt; annars blir man tvungen att gå över en bro man redan gått på en gång för att komma därifrån sista gången punkten besöks. En promenad kan bara ha en start- och en slutpunkt.
I fallet Königsberg har alla fyra punkter ett udda antal förbindelser och ingen lösning är därför möjlig i detta fall.
Utan att visa det konstaterade Euler även att
- om det finns exakt två noder med ett udda antal förbindelser så finns det en lösning där promenaden börjar i någon av dessa punkter och slutar i den andra.
- om ingen nod har ett udda antal förbindelser så går det att hitta en promenad som passerar varje bro exakt en gång oavsett vilken punkt som är startpunkt.
Det andra påståendet bevisades 1873 av den tyske matematikern Carl Hierholzer. Han visade att det finns en lösning oavsett i vilken punkt man startar och promenaden börjar och slutar i samma punkt.
Till minne av Euler kallar man en sådan promenad som passerar alla broar exakt en gång för en Eulerväg. Om promenaden börjar och slutar i samma punkt kallas den för en Eulercykel.
Övrigt

Notera skillnaden mellan kartan över Königsberg från Eulers tid, som visar det verkliga utseendet på Königsbergs centrala delar, och den schematiska bilden. Skillnaden mellan dessa tydliggör hur topologin bortser från oväsentliga egenskaper hos de objekt som studeras.
De sju broarna hade under den tyska tiden egna namn. Broarna till den norra stranden hette, räknat från väster Krämerbrücke, ("Krämarbron"), Schmiedbrücke ("Smedbron"), och Holzbrücke ("Träbron"), broarna till den södra stranden hette, räknat från väster, Grünbrücke ("Gröna bron"), Köttelbrücke ("Kråsbron") och Höhebrücke ("Högbron"), medan bron mellan de två öarna hette Honigbrücke ("Honungsbron"). I dagens Kaliningrad finns det bara fem broar kvar, och av dessa är endast två stycken, Holzbrücke och Höhebrücke, kvar från Eulers tid. Honigbrücke ersattes 1935 av en ny bro, medan Schmiedbrücke och Köttelbrücke förstördes under andra världskriget. De två ursprungliga västliga broarna, Krämerbrücke och Grünbrücke, revs av ryssarna efter kriget och ersattes av en gemensam bro, vilket därmed gjorde den önskade promenaden möjlig.
Se även
| Den här artikeln ingår i boken: Grafteori |
Referenser
- James R. Newman (Ed.). The World of Mathematics, volume I. Simon and Schuster, New York, 1956.
- Newmans antologi finns översatt till svenska som SIGMA: En matematikens kulturhistoria , svensk red. Tord Hall (1959, flera upplagor). Eulers översatta artikel om broproblemet finns i band IV av den svenska utgåvan.
Noter
- ^ Euler, Leonhard (1726). Commentarii Academiae scientiarum imperialis Petropolitanae. Petropolis, Typis Academiae. http://archive.org/details/commentariiacade08impe. Läst 15 april 2023
Externa länkar
- Königsberg bridges (engelska)
- A visit at the bridges of Königsberg (engelska)
Media som används på denna webbplats
Based on X-office-address-book.svg.
Författare/Upphovsman: Bogdan Giuşcă, Licens: CC BY-SA 3.0
The problem of the Seven Bridges of Königsberg.








