Jämna och udda funktioner

Den här artikeln behöver källhänvisningar för att kunna verifieras. (2020-03) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan.

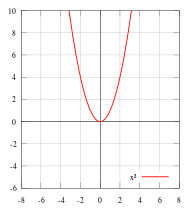
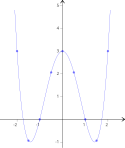
Jämna och udda funktioner är matematiska funktioner som uppfyller vissa symmetrivillkor. En funktion ƒ(x) är jämn om ƒ(-x) = ƒ(x), udda om ƒ(-x) = -ƒ(x).

Jämna funktioners grafer är alltså symmetriska under spegling i y-axeln, medan udda funktioners är symmetriska under 180° rotation kring origo.

Namnen motiveras bland annat av att funktionerna ${\displaystyle x^{n}}$ för jämna n är jämna funktioner och udda för udda n, samt av att maclaurinutvecklingen av en jämn funktion bara har termer med jämna exponenter, och motsvarande för udda.

Exempel

Jämna funktioner:

• ${\displaystyle f(x)=x^{2}\,}$
• ${\displaystyle f(x)=\left|x\right|}$
• ${\displaystyle f(x)=\cos(x)\,}$
• Dirichlets funktion

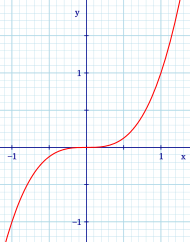
Udda funktioner:

• ${\displaystyle f(x)=x\,}$
• ${\displaystyle f(x)=x^{3}\,}$
• ${\displaystyle f(x)=\sin x\,}$

Egenskaper

• Den enda funktionen som är både jämn och udda är den konstanta funktionen ${\displaystyle f(x)=0}$.
• Summan av en udda och en jämn funktion är varken udda eller jämn, såvida inte en av funktionerna är konstant noll.
• Summan av två udda funktioner är udda, och varje multipel av en udda funktion är udda.
• Summan av två jämna funktioner är jämn, och varje multipel av en jämn funktion är jämn.
• Produkten av både två udda eller två jämna funktioner är en jämn funktion.
• Produkten av en udda och en jämn funktion är en udda funktion.
• Kvoten av både två udda eller två jämna funktioner är jämn.
• Kvoten av en jämn och en udda funktion är udda.
• En sammansatt funktion av två udda funktioner är udda. En sammansättning av två jämna funktioner är jämn.
• En sammansatt funktion av en udda och en jämn funktion är jämn.
• Derivatan av en jämn funktion är udda (förutsatt att funktionen är deriverbar).
• Derivatan av en udda funktion är jämn (förutsatt att funktionen är deriverbar).
• Integralen av en udda funktion från -a till a är noll, dvs om f är udda:

${\displaystyle \int _{-a}^{a}f(x)dx=0}$

• Integralen av en jämn funktion från -a till a är två gånger integralen från noll till a, dvs om g är jämn:

${\displaystyle \int _{-a}^{a}g(x)dx=2\int _{0}^{a}g(x)dx}$

Se även

• Paritet