Heap (datastruktur)

Den här artikeln behöver källhänvisningar för att kunna verifieras. (2023-07) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan.

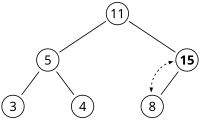
Ett partiellt ordnat vänsterbalanserat träd (engelska: heap) är en datastruktur, närmare bestämt ett träd, som karakteriseras av att

• varje nods värde är större eller lika med värdena i nodens barn (partiellt ordnat).
• trädets grenar är så lika långa som möjligt. I fall det inte är möjligt så fylls den nedersta nivån på från vänster (vänsterbalanserat).

Detta kallas ibland för en max-heap, alternativt kan man implementera en heap så att varje nods värde är mindre eller lika med nodens barns värden, en sådan heap kallas min-heap.

Namnet heap kommer från att det faktum att trädet är vänsterbalanserat gör det implementerbart i ett sammanhängande minnesområde, till exempel en minnesheap eller array. Nivå k i ett träd där varje nod har b barn, räknat med roten som 0, har ${\displaystyle b^{k}}$ noder. Första noden på nivån har position ${\displaystyle {\frac {b^{k}-1}{b-1}}}$ indexerat från 0. Alltså går det att räkna ut var i minnet en viss nod finns lagrad, om trädet har minst så många noder.

Detta i kombination med partiell ordning gör operationen att upprepade gånger "plocka" det största talet ur trädet billig, samtidigt som nya element och uppdateringar är effektiva. Den är därför lämplig som exempelvis prioritetskö för jobb.

Binär heap

I en binär heap har varje nod två barn, det vill säga att heapen är ett binärt träd. Detta implementeras oftast i en array, där roten har plats noll och nod k har sina barn på plats 2k + 1 respektive 2k + 2. En nods k förälder kan nås genom att avrunda (k - 1)/2 neråt till närmaste heltal. Att läsa elementen i en array är som att läsa det binära trädet vänster till höger, uppifrån och ner.

Insättande av element

I en binär max-heap läggs ett nytt element till på följande sätt:

1. Lägg till det nya elementet till den nedersta nivån i den första lediga platsen till vänster.
2. Jämför det nytillagda elementet med sin föraldranod. Är föräldranodens värde större, sluta.
3. Om inte, byt plats på noderna och upprepa steg 2.

	Steg 1	Steg 2/3	Steg 3/3
Heap
Array	${\displaystyle [11~~5~~8~~3~~4~~X]}$	${\displaystyle [11~~5~~15~~3~~4~~8]}$	${\displaystyle [15~~5~~11~~3~~4~~8]}$
Beskrivning	Ett nytt element X läggs till. I det här fallet är X lika med 15.	15 är större än 8, så noderna byter plats.	15 är större än 11, så noderna byter plats. 15 är nu ny rot, och har därmed ingen föräldranod, så insättningen är klar.

Borttagande av roten

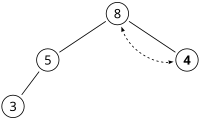
Borttagande av roten på en binär max-heap går till på följande sätt:

1. Ta bort roten. Ta noden B som är längst ner, längst till höger och sätt i rotens ställe.
2. Om B är större än sina barn, sluta.
3. Annars, byt plats på B och det största av dess barn. Gå tillbaka till steg 2.

	Steg 1	Steg 2/3
Heap
Array	${\displaystyle [4~~5~~8~~3]}$	${\displaystyle [8~~5~~4~~3]}$
Beskrivning	Roten tas bort och elementet 4 tar dess plats.	Båda barnen (5 och 8) är större än 4. 8 är större än 5, så 8 och 4 byter plats. 4 har nu inga barn, så borttagandet är klart.

Se även

• Heap (mikroprocessor)
• Prioritetskö
• Stack (datastruktur)