Hassediagram

Inom ordningsteori är ett Hassediagram ett slags matematiskt diagram som används för att representera en ändlig partialordnad mängd ("pomängd") som ett nätverksdiagram över dess täckningsrelation. För en partiellt ordnad mängd (S, ≤) representeras varje element i S som ett hörn i planet och en kant sammanbinder hörnet x uppåt med alla hörn y som täcker x, det vill säga närhelst x < y och det inte finns något z sådant att x < z < y. Dessa kanter får korsa varandra men ej passera några andra hörn än sina respektive ändpunkter. Ett sådant diagram med betecknade hörn beskriver mängdens partiella ordning på ett unikt sätt.

Hassediagram är uppkallade efter Helmut Hasse (1898–1979) enligt Birkhoff (1948) och de kallas så på grund av Hasses användning av dem. Det var dock inte Hasse som använde dem först, de förekommer exempelvis i Vogt (1895). Fastän Hassediagram ursprungligen designats för att rita grafer över pomängder för hand, har de på senare tid konstruerats automatiskt.^[1]

Ett "bra" Hassediagram

Fastän Hassediagram är enkla likväl som intuitiva verktyg för hantering av finita pomängder, visar det sig vara ganska svårt att rita "bra" diagram. Anledningen till detta är att det i allmänhet finns många möjliga sätt att rita ett Hassediagram för en pomängd. Den enkla metoden att bara börja med de minsta elementen och sedan fortsätta uppåt med större element i ordning ger ofta ganska dåliga resultat: symmetrier och interna strukturer går lätt förlorade.

Nedanstående exempel visar problemet. Betrakta potensmängden (mängden av delmängder) av en mängd med fyra element som ordnas efter inklusivitet (om de är delmängder av en mängd med ett element mer). Varje delmängd har en nod som är fyrställigt betecknad med huruvida ett element ingår i delmängden (1) eller ej (0):

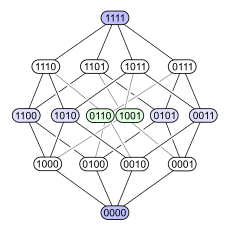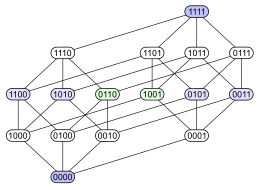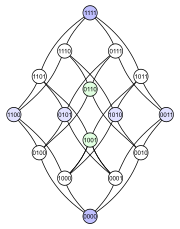Det första diagrammet visar tydligt att potensmängden är rangordnad efter hur många element som ingår (antalet ettor). Det andra diagrammet har samma rangordnade struktur, men genom att förlänga vissa kanter förstärker man intrycket av att strukturen är en tesserakt, som är en förening av två tredimensionella kuber. Det tredje visar en del av den inre strukturen (andra och tredje positionerna "värderas högre" än första och fjärde) och i det fjärde är hörnen i den tredje arrangerade som en 4×4-matris.

Exempel

Delbarhetsgitter

Med Hassediagram kan man framställa sambanden mellan olika faktoriseringar. I diagrammet nedan visas de tal som kan bildas genom multiplikation av två, tre och fem. Med utgångspunkt i hörnet representerande ett längst ner leder kanter uppåt till 1⋅2=2, 1⋅3=3 och 1⋅5=5. Därifrån nya kanter till hörn representerande resultatet av dessa tal multiplicerade med två, tre respektive fem, etcetera. Man kan fylla på med ytterligare primtal (7, 11, 13...), men bilden blir strax ganska gyttrig.

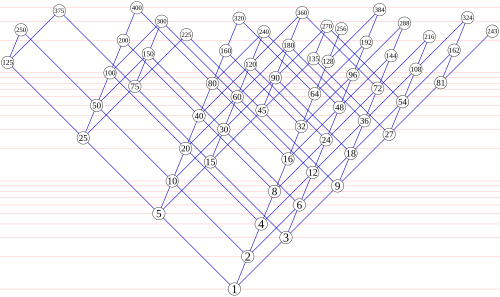
Partitioner av mängder

Hassediagram över partitioner av en mängd med fyra element sorterade efter "finhet". Med "finhet" avses här att en partition P är finare än en partition Q om varje element i P är en delmängd till ett element i Q. Om vi börjar nerifrån i det vänstra diagrammet nedan, så utgår vi från alla de fyra partitionerna av storleken ett: {1},{2},{3},{4}. Slår vi ihop två av dessa partitioner, vilket ju kan göras på sex olika sätt, får vi partitionerna i raden ovanför så att vi nu har tre partitioner. Slå ihop två av dessa tre partitioner, vilket kan göras på tre sätt varför det finns tre kanter uppåt från varje, och vi har två partitioner kvar (som kan se ut på sju olika sätt - 3+1 på fyra sätt och 2+2 på tre - beroende på vilken väg vi hittills valt). Dessa slås till slut ihop till hela {1,2,3,4} i diagrammets topp. I det högra diagrammet visas "redundanta" kanter med rött - kanter som förvisso uppfyller finhetskravet, men där det finns mellanliggande hörn så att kanterna därför ej ingår i Hassediagrammet.

Referenser

Noter

Källor

• Baker, K. A.; Fishburn, P.; Roberts, F. S. (1971), ”Partial orders of dimension 2”, Networks 2 (1): 11–28, doi:10.1002/net.3230020103 .
• Bertolazzi, R; Di Battista, G.; Mannino, C.; Tamassia, R. (1993), ”Optimal upward planarity testing of single-source digraphs”, Proc. 1st European Symposium on Algorithms (ESA '93), Lecture Notes in Computer Science, "726", Springer-Verlag, s. 37–48, doi:10.1007/3-540-57273-2_42 .
• Birkhoff, Garrett (1948), Lattice Theory (Revised), American Mathematical Society .
• Chan, Hubert (2004), ”A parameterized algorithm for upward planarity testing”, Proc. 12th European Symposium on Algorithms (ESA '04), Lecture Notes in Computer Science, "3221", Springer-Verlag, s. 157–168, https://link.springer.com/chapter/10.1007/978-3-540-30140-0_16 .
• Di Battista, G.; Tamassia, R. (1988), ”Algorithms for plane representation of acyclic digraphs”, Theoretical Computer Science 61 (2–3): 175–178, doi:10.1016/0304-3975(88)90123-5 .
• Freese, Ralph (2004), ”Automated lattice drawing”, Concept Lattices, Lecture Notes in Computer Science, "2961", Springer-Verlag, s. 589–590 . Ett utökat förtryck finns online på: [1].
• Garg, Ashim; Tamassia, Roberto (1995a), ”Upward planarity testing”, Order 12 (2): 109–133, doi:10.1007/BF01108622 .
• Garg, Ashim; Tamassia, Roberto (1995b), ”On the computational complexity of upward and rectilinear planarity testing”, Graph Drawing (Proc. GD '94), LectureNotes in Computer Science, "894", Springer-Verlag, s. 286–297, doi:10.1007/3-540-58950-3_384 .
• Jünger, Michael; Leipert, Sebastian (1999), ”Level planar embedding in linear time”, Graph Drawing (Proc. GD '99), Lecture Notes in Computer Science, "1731", s. 72–81, doi:10.1007/3-540-46648-7_7, ISBN 978-3-540-66904-3 .
• Vogt, Henri Gustav (1895), Leçons sur la résolution algébrique des équations, Nony, s. 91 .