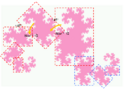
Harter-Heighways drakkurva

Harter-Heighways drakkurva är en drakkurva, först undersökt av William Harter, John Heighway och Bruce Banks på 1960-talet. De arbetade då som fysiker vid NASA. Stora delar av Harter-Heighways drakkurvas egenskaper publicerades först av Chandler Davis och Donald Knuth. Denna kurva kallas ibland även för "Jurassic Park–draken" då iterationer av den förekom i Michael Crichtons bok Jurassic Park.

Egenskaper

Harter-Heighways drakkurva är en linjär drakkurva. Det är en kurva som tangerar sig själv men aldrig korsar sig själv.

Fraktaldimension

Trots att den här kurvan har ett komplicerat utseende består den av enkla element och har enkla dimensioner.
Dess fraktaldimension är ${{\frac {\ln 2}{\ln {\sqrt {2}}}}=2}$ .

Kurvans yta är även den av ganska enkla förhållanden: om vår startbit var 1 längdenhet lång kommer vår slutgiltiga yta att gå mot att $\textstyle {\frac {1}{2}}$ areaenheter. Kurvans gränslinjer kommer att vara oändligt långa då de ökar med ${\sqrt {2}}$ för varje iteration.

Likheter inom kurvan

Det går att hitta en del upprepningar inom drakkurvan. Till exempel att vi får en repetition av samma mönster som har blivit förminskat med ${\sqrt {2}}$ och blivit vridet med 45° gentemot den liknande föregående mönsterdelen (mönsterdelarna är i bilden nedan inrutade med fyrkanter).

Om man sedan ta ut en av dessa mönsterdelar ser vi att den i sin tur är en hel drakkurva i mindre format. Detta kommer att visa sig gälla för alla dessa mönsterdelar oavsett hur små de blir då vi har itererat vår kurva ett oändligt antal gånger.

Att skapa Harter-Heighways drakkurva

Det finns flera olika sätt att skapa en Harter-Heighway drakkurva. Man kan göra det genom att vika papper enligt ett speciellt mönster. Det kan även göras genom att använda sig av linjer som man sedan använder sig av för att bygga upp drakkurvan.

Vika en drakkurva

När man vill skapa en Harter-Heighway drakkurva genom att vika papper börjar man genom att ta en remsa med styvt papper. Det ska vara ett lite styvare papper på grund av att det stannar i den form man vill bättre än ett ostyvt papper. Sedan viker man detta papper på mitten, sedan viker man det på mitten igen och viker det på mitten igen och så vidare så här. Ihopvikningen skall göras åt samma håll hela tiden. Om man viker sitt papper n gånger får man en drakkurva av n:te-graden. När man sedan har vikt sitt papper så många gånger man vill skall man börja vika upp det. Det skall då vikas upp med 90 graders vinklar överallt. Man viker upp sin hopvikta del som bilden nedan visar.

Bygga upp en drakkurva med linjer

Att bygga en Harter-Heighway drakkurva med linjer gör man på så vis att man börjar med en rät linje. Det man sedan gör med denna linje är att man kan se det som om man trycker ut linjen så att den bildar en rätvinklig triangel med den gamla linjen som bas. Detta fortsätter man sedan att göra för de allt mindre linjerna; man trycker linjerna mot vartannat håll, varannan inåt och varannan utåt, så som bilden nedan visar.

(c) Romero Schmidtke, CC BY-SA 3.0

Här är en länk til ett annat sätt att skapa en Harter-Heighway drakkurva

Ihop-passning av Harter-Heighway drakkurvor

Det går att passa ihop flera av dessa kurvor så att man skapar en sammanhängande mosaik där ingen av kurvorna korsar varandra någonstans utan de bara tangerar varandra. Bland annat så kan dessa bilder skapas.

1:a med 4 drakkurvor
2:a med 4 drakkurvor
3:e med 4 drakkurvor
4:e med 4 drakkurvor
1:a med 2 drakkurvor
2:a med 2 drakkurvor (tvillingdrake)
3:e med 2 drakkurvor
1:a Exemplet på plan utfyllnad
2:a Exemplet på plan utfyllnad
3:e Exemplet på plan utfyllnad