Gregoryteleskop

Strålgången i ett Gregoryteleskop. Primärspegeln (ljusblå), med hål i mitten, till höger.
Strålgången i ett Cassegrainteleskop. De gröna strålarna från det lägre liggande objektet fokuseras i en punkt ovanför de violetta strålarna från det övre objektet, så att bilden roteras 180°.
Strålar (röda) som går genom det ena fokuset hos en elliptisk spegel, återsamlas i det andra.
Ett Cassegrainteleskop har en hyperbolisk sekundärspegel. Strålar riktade mot F1 sammanfaller i F2.

Ett Gregoryteleskop[1], ibland kallat Gregorys teleskop[2] eller gregorianskt teleskop[3], är en spegelteleskopskonstruktion som beskrevs av den skotske matematikern och astronomen James Gregory 1663[4].

Det första Gregoryteleskopet konstruerades av Robert Hooke 1673, dock med sfäriska speglar.[5] James Short var, på 1730-talet, den förste att tillverka ett "klassiskt" Gregoryteleskop med paraboloidal primärspegel och ellipsoidal sekundärspegel och han tillverkade under sin levnad gott och väl ettusen exemplar.[6]

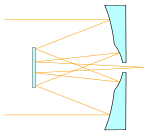
I ett Gregoryteleskop reflekteras det infallande ljuset först i en primärspegel och detta reflekterade ljus reflekteras sedan tillbaka mot primärspegeln av en sekundärspegel. Primärspegeln är dock, i sin "klassiska" utformning, försedd med ett centralt hål genom vilket det återreflekterade ljuset passerar.

Gregoryteleskopet påminner om Cassegrainteleskopet, men till skillnad från detta är båda speglarna konkava (sekundärspegeln i ett Cassegrainteleskop är konvex, i sin "klassiska" utformning hyperboloidal[7]).[8] Gregoryteleskopets, liksom Cassegrainteleskopets, primärspegel är, i den "klassiska" utformningen, parabolisk med sitt fokus mellan primär- och sekundärspegeln (i Cassegrinteleskopet har primärspegeln sitt fokus bortom sekundärspegeln), medan sekundärspegeln är prolat ellipsoidal med sitt ena fokus placerat i primärspegelns fokus, och bilden skapas därmed i sekundärspegelns andra fokalplan[9]. Att konstruktionen har två fokus gör att bilden blir rättvänd.[10] Detta "extra" fokus mellan speglarna gör också att man kan sätta in en fältbländare för att minska mängden strålning som når sekundärspegeln, och fältbländare (som kan vara försedda med kylning och avledande speglar) utnyttjas i solteleskop för att minska uppvärmningen.[11][12]

Till Gregoryteleskopets fördelar hör den rättvända bilden och att en fältbländare kan monteras, till Cassegrainteleskopets fördelar att det är kortare[13] (och en rättvänd bild kan ordnas med ett dubbelt porroprisma). Därutöver är Gregoryteleskopets sekundärspegel enklare att tillverka.[14]

Gregoryteleskopen är enklare att kollimera och de var populärare än Cassegrainteleskop fram till 1800-talets mitt. Gregoryteleskop används fortfarande till annat än solteleskop och ett användningsområde är som sökare med rättvänd bild på större teleskop.

Gregorys konstruktionsprincip (liksom Cassegrains) används även för parabolantenner.

  • Genom att placera en plan spegel mellan primär- och sekundärspeglarna i ett Gregoryteleskop och sedan integrera sekundärspegeln i primärspegeln, kan teleskopets längd halveras.
    Genom att placera en plan spegel mellan primär- och sekundärspeglarna i ett Gregoryteleskop och sedan integrera sekundärspegeln i primärspegeln, kan teleskopets längd halveras.
  • Gregoryteleskop från cirka 1735.
    Gregoryteleskop från cirka 1735.
  • Gregoryteleskop från cirka 1748. Notera anordningen på sidan för att med hjälp av en skruv flytta sekundärspegeln framåt och bakåt i tuben för skärpeinställning.
    Gregoryteleskop från cirka 1748. Notera anordningen på sidan för att med hjälp av en skruv flytta sekundärspegeln framåt och bakåt i tuben för skärpeinställning.
  • Goode Solar Telescope vid Big Bear Solar Observatory i Kalifornien är ett excentriskt[15] Gregoryteleskop med 1,6 meters fri apertur och var därmed världens största 2009.[16][17][18]
    Goode Solar Telescope vid Big Bear Solar Observatory i Kalifornien är ett excentriskt[15] Gregoryteleskop med 1,6 meters fri apertur och var därmed världens största 2009.[16][17][18]
Om objektet (den stora röda pilen till vänster) befinner sig på ändligt avstånd (varav större delen klippts bort mellan sicksacklinjerna) kan man flytta sekundärspegeln (M2) bort från primärspegeln (M1) så att bilden hamnar i samma fokalplan (F) som om objektet befann sig på oändligt avstånd (då sekundärspegelns närmsta fokus, F2, skulle sammanfallit med primärspegelns fokus, F1, bildplanet , F, hade sammanfallit med sekundärspegelns bortre fokus, också detta markerat F2, och sekundärspegeln hade då skolat befinna sig där den röda konturen anger). Figuren visar gröna konstruktionslinjer för primärspegelns bild (en pytteliten uppochnervänd pil mellan F2 och F1), blå konstruktionslinjer för sekundärbilden ur primärbilden och en gul stråle från objektets pilspets, via primärbildens pilspets, till slutbildens pilspets i F. Speglarnas diametrar och hålet i primärspegeln är överdrivna i förhållande till fokallängden för att tydliggöra strålgången (vilket dock också leder till ganska tydliga komaeffekter, vilka ignorerats vid ritandet av den gula stålen).

Referenser

Noter

  1. ^ Gregoryteleskop i Nationalencyklopedin
  2. ^ Gregorys teleskop i Nordisk familjebok, uggleupplagan 1909, band 10, spalt 197.
  3. ^ Jämför engelska Gregorian telescope. Benämningen på svenska är dock tämligen misslyckad, eftersom den snarare för tankarna till påven Gregorius den store, påve 590 till 604 f.Kr. eller Gregorius XIII som införde den gregorianska kalendern 1582. Även stavningen "gregorysk" ses ibland.
  4. ^ J. Gregory, 1663, Optica Promota, Samuel Thomson för John Hayes, London (teckning av teleskopet på sid. 94). Propositio 52-59 (med engelsk översättning och kommentarer av Ian Hayes).
  5. ^ Wilson Wall, 2018, A History of Optical Telescopes in Astronomy, sid. 68. ISBN 9783319990880.
  6. ^ James Short's Reflecting Telescopes på National Museums Scotland. Se även V. Sacek.
  7. ^ En hyperbolisk spegel har två brännpunkter. Strålar riktade mot den inre brännpunkten sammanstrålar i den yttre.
  8. ^ I tidiga teleskop använde man dock sfäriska speglar på grund av tillverkningssvårigheterna. Den första (ungefärligt) paraboliska spegeln tillverkades 1721 av John Hadley (till ett Newtonteleskop som har en plan sekundärspegel). Se Early Reflectors på Tools of Cosmology.
  9. ^ Sekundärspegeln har formen av ena änden av en ellips som roteras längs storaxeln. En ellips har två fokus som båda ligger på storaxeln och sålunda har även den prolata rotationsellipsoiden det.
  10. ^ Det extra fokuset fungerar som ett symmetricentrum. Upp blir ner och höger blir vänster (och vice versa), det vill säga en bildrotation på 180°.
  11. ^ GREGOR Arkiverad 15 mars 2019 hämtat från the Wayback Machine. på Leibnitz-Institut for Sonnenphysik.
  12. ^ Yoshinori Suematsu; Yukio Katsukawa; Toshifumi Shimizu; Kiyoshi Ichimoto, 2017, Instrument design of 1.5-m aperture solar optical telescope for the Solar-C Mission, Proceedings Volume 10564, International Conference on Space Optics — ICSO 2012; 105640T (2017) doi:10.1117/12.2309169.
  13. ^ Som framgår av figurerna är längden på ett Gregoryteleskop lika med summan av de båda speglarnas fokallängder, medan ett Cassegrainteleskops längd är kortare än primärspegelns fokallängd.
  14. ^ Lloyd Jones, Kapitel 18: Reflective and Catadiopric Objectives Arkiverad 12 juli 2019 hämtat från the Wayback Machine., sid. 18.11 - 18.12 i Michael Bass (ed.), 2002, Handbook of optics, volym 2. ISBN 0-07-047974-7.
  15. ^ Med en konstruktion som inte är symmetrisk i förhållande till speglarnas optiska axlar
  16. ^ BBSO New Telescope
  17. ^ World's largest solar telescope now operational, Astronomy, 29 maj 2009.
  18. ^ Världens största solteleskop, Daniel K. Inouye Solar Telescope, är nu under byggnad på Maui och väntas stå färdigt 2020. Det har en primärspegel på fyra meter, en sekundärspegel på 62 cm och är även detta ett excentiskt Gregoryteleskop. Se DKI Solar telescope, Feed Optics, DKIST - Top End Optical Assembly och M1 - Primary Mirror på National Solar Observatory.

Externa länkar

Media som används på denna webbplats

Cassegrain Telescope.svg
Författare/Upphovsman: Krishnavedala, Licens: CC BY-SA 4.0
Diagram of the lightpath through a Cassegrain telescope.
Propriete reflexion ellipse tangente bissectrice.svg
Författare/Upphovsman: Christophe Dang Ngoc Chan (Cdang (talk)), Licens: CC BY-SA 3.0
Relationship between the tangent and the bisecting line of an ellipse, and the resulting point-to-point focalisation on an elliptic mirror. Eccentricity: e = 0.866.
GST dome inside.jpg
Författare/Upphovsman: Pgoode1943, Licens: CC BY-SA 4.0
Image of GST Dome
Hyperbolic mirror.svg
Författare/Upphovsman: Episcophagus, Licens: CC BY-SA 4.0
Hyperbolic mirror blue. Yellow rays directed to red focus F1 are reflected and intersect in red focus F2.
Modified gregorian.svg
Författare/Upphovsman: Episcophagus, Licens: CC BY-SA 4.0
By putting a plane mirror between the primary and secondary mirrors, and then integrate the secondary in the primary, the total length of a gregorian telescope can be reduced.
Gregorian reflecting telescope, Johann Gottlob Rudolph, Miltitz, c. 1748 - Mathematisch-Physikalischer Salon, Dresden - DSC07986.JPG
Exhibit in the Mathematisch-Physikalischer Salon (Zwinger), Dresden, Germany. This artwork is old enough so that it is in the public domain. Photography was permitted in the museum without restriction.
Gregorian telescope circa 1735 in Putnam Gallery 2, 2009-11-24.jpg
Författare/Upphovsman: Sage Ross, Licens: CC BY-SA 3.0
Kameraposition42° 22′ 35,43″ N, 71° 06′ 57,87″ V Kartographer map based on OpenStreetMap.Se denna och andra närliggande bilder på: OpenStreetMapinfo
A Gregorian telescope of English manufacture circa 1735, owned by John Winthrop, on display at the Putnam Gallery in the Harvard Science Center
Gregorian telescope.svg
Författare/Upphovsman: Krishnavedala, Licens: CC BY-SA 4.0
Diagram of the lightpath through a Gregorian telescope.
Gregory telescope - finite distance to object.svg
Författare/Upphovsman: Episcophagus, Licens: CC BY-SA 4.0
A red arrow at a finite distance from a gregorian telescope focused in the same plane (F) as if it was at infinite distance by moving the elliptical secondary mirror (M2) the distance d away from the parabolical primary mirror (M1). Green dotted lines for construction of primary image and blue dotted lines for constructing secondary image from primary image. Yellow line shows an actual light-ray through telescope. Red line shows optical axis. Red contour shows location of secondary mirror if the object was at infinite distance, so that focus of primary (F1) and close focus of secondary (F2) coincide and distant focus of secondary (also marked F2) coincide with wanted projective plane of telesocpe (F). Black zig-zag lines symbolize a lot of "cropped distance". Vertical size of secondary mirror and aperture in primary mirror exaggerated, else the lines would have been indistinguishably cluttered, and the figure is cluttered enough as it is.