Gravitationell singularitet
En gravitationell singularitet är en punkt i rumtiden där de värden som beskriver ett gravitationsfälts styrkor får oändliga värden, och allmänt vedertagna fysikaliska lagar upphör att vara användbara för att beskriva tillståndet i singulariteten. En sådan lag är Newtons gravitationslag. I singularitetsfallet innebär detta att två massor upptar samma plats, och avståndet mellan kropparna är således 0. Detta får till följd att
Den vanligaste manifestationen av gravitationella singulariteter torde vara svarta hål där den faktiska singulariteten döljs av en händelsehorisont.
Uppkomst
I fallet svarta hål är en gravitationell singularitet en lösning där den allmänna relativitetsteorin kombineras med Paulis uteslutningsprincip. Materiens grundläggande byggstenar, kvarkar och elektroner, har i sig själva ingen bestämd storlek, men arrangerar sig normalt med ett visst minsta avstånd då detta är energimässigt fördelaktigt. Under inverkan av mycket höga tryck kan det bli energimässigt fördelaktigt för flera partiklar att dela på samma utrymme och istället arrangera sig på olika energinivåer, så kallad degenererad materia. En singularitet inträffar i det extrema specialfallet att degenerationstrycket helt övervinns och alla partiklar samlas i en och samma punkt (eller i en ring om materien har ett rörelsemängdsmoment).
Kritik
Singulariteter brukar inom fysiken tolkas som en saknad pusselbit i förståelsen av ett fenomen. De flesta teoretiker menar att den allmänna relativitetsteorin i sin nuvarande form inte är giltig på mycket korta avstånd och att andra fenomen blir aktuella när en partikel närmar sig centrum.
Se även
Media som används på denna webbplats
(c) I, Dennis Nilsson, CC BY 3.0
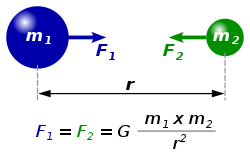
This diagram describes the mechanisms of Newton's law of universal gravitation; A point mass m1 attracts another point mass m2 by a force F2 pointing along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance (r) between the point masses. Regardless of masses or distance, the magnitudes of the two forces, |F1| and |F2| (absolute values), will always be equal. G is the gravitational constant; G ≈ 6.67428(67)×10−11 m3/(kg·s2).