Golv- och takfunktionerna
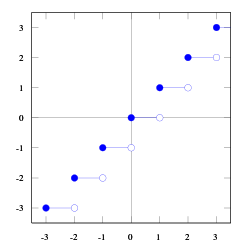

Golv- och takfunktionerna är två funktioner inom talteorin.
Värdet av golvfunktionen för något reellt tal x är det största heltal som är mindre än eller lika med x (för positiva tal x ger golvfunktionen helt enkelt heltalsdelen av x).
Exempel:
Andra beteckningssätt är (av engelska floor ’golv’) och
Takfunktionen ger på motsvarande sätt det minsta heltal som är större än eller lika med x.
Exempel:
Ett annat beteckningssätt är (av engelska ceiling ’(inner)tak’).
Egenskaper
Srinivasa Aiyangar Ramanujan presenterade följande problem i Journal of the Indian Mathematical Society.[1]
Om n är ett positivt heltal, bevisa att
(i)
(ii)
(iii)
Användningar
Formler för primtal
Talet n är ett primtal om och endast om[2]
Låt r > 1 vara ett heltal, pn det n-te primtalet, och
Då är[3]
Det finns ett tal θ = 1.3064... (Mills konstant) så att
är alla primtal.[4]
Det finns även ett tal ω = 1.9287800... med egenskapen att
är alla primtal.[4]
Om π(x) är antalet primtal mindre eller lika stora som x, får man följande formel som en enkel konsekvens av Wilsons sats:[5]
Om n ≥ 2, är[6]
Ingen av formlerna i denna sektion är dock av någon praktisk betydelse.[7][8]
Se även
Referenser
- ^ Ramanujan, Question 723, Papers p. 332
- ^ Crandall & Pomerance, Ex. 1.3, p. 46
- ^ Hardy & Wright, § 22.3
- ^ [a b] Ribenboim, p. 186
- ^ Ribenboim, p. 181
- ^ Crandall & Pomerance, Ex. 1.4, p. 46
- ^ Ribenboim, p.180 says that "Despite the nil practical value of the formulas ... [they] may have some relevance to logicians who wish to understand clearly how various parts of arithmetic may be deduced from different axiomatzations ... "
- ^ Hardy & Wright, pp.344—345 "Any one of these formulas (or any similar one) would attain a different status if the exact value of the number α ... could be expressed independently of the primes. There seems no likelihood of this, but it cannot be ruled out as entirely impossible."
Externa länkar
 Wikimedia Commons har media som rör Golv- och takfunktionerna.
Wikimedia Commons har media som rör Golv- och takfunktionerna.
Media som används på denna webbplats
Författare/Upphovsman: Ingen maskinläsbar skapare angavs. Omegatron (diskussion · bidrag) antaget (baserat på upphovsrättsanspråk)., Licens: CC BY-SA 3.0
Graph of the floor function.
Författare/Upphovsman: Omegatron, Licens: CC BY-SA 3.0
Den här W3C-ogiltig vektorbilden skapades med Gnuplot.

