Gauss lag

Den här artikeln behöver källhänvisningar för att kunna verifieras. (2020-10) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan.

I fysiken syftar Gauss lag på någon tillämpning av den generella matematiska satsen Gauss sats som ger sambandet mellan ytintegralen av något flöde, till exempel av vätska, som flödar ut ur en sluten yta och resultatet av källor som är inneslutna i den slutna ytan. Gauss lag används oftast inom elektrostatik och magnetostatik.

• 
  Det integrerade flödet är proportionellt mot de inneslutna källornas styrka.
• 
  Utan källor eller sänkor är det integrerade flödet noll.
• 
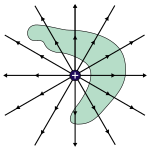
  Flödets ytintegral för en dipol är noll.

Gauss sats åberopas särskilt inom elektrostatik för sambandet mellan elektrisk laddning (enhet coulomb) och elektrisk flödestäthet (enhet C/m²) eller elektrisk fältstyrka (enhet V/m). Den säger då att den totala laddning som finns innanför en sluten yta är lika med ytintegralen av den elektriska flödestätheten över hela ytan, som figuren (a) visar ovan. Om laddningen innanför är en punktformig laddning leder detta till Coulombs lag.

Ingen magnetisk monopol har någonsin hittats, vilket betyder att magnetfält inte har några källor i den mening som används ovan. Gauss lag för magnetiska fält säger därför att ytintegralen av det magnetiska fältet över en sluten yta alltid är noll: det kan aldrig finnas någon magnetisk laddning att innesluta. En följd av detta är att magnetiska fältlinjer alltid är slutna (dvs inte har några ändar). Bilderna (a) och (b) ovan kan därför inte visa magnetiska fält, medan dipolfältet i (c) kan existera.

• Carl Friedrich Gauss

• Wikimedia Commons har media som rör Gauss lag.
  Bilder & media