Fotpunkt

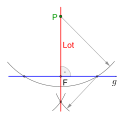
Inom matematiken är fotpunkt en beteckning för skärningspunkten mellan en given linje eller yta och normalen till denna linje/yta genom en given punkt, det vill säga punktens vinkelräta projektion på linjen eller planet. Fotpunkt är även beteckning på utgångspunkten för en vektorpil.^[1]

Med fotpunktstriangel menas den triangel (${\displaystyle \triangle LMN}$ i figur 2) som har sina hörn i en punkts (${\displaystyle P}$) fotpunkter på en annan triangels (${\displaystyle \triangle ABC}$) sidor (eller förlängningar av dessa). Om punkten ligger på den omskrivna cirkeln till ${\displaystyle \triangle ABC}$ ligger de tre fotpunkterna i stället på en linje, Simsons linje.

Med fotpunktscirkel avser man den omskrivna cirkeln till fotpunktstriangeln.

Referenser

Fotpunkt i Nordisk familjebok (Uggleupplagan).