Fermi–Dirac-statistik

Fermi-Dirac-funktionens temperaturberoende

Fermi-Dirac-statistik, uppkallad efter fysikerna Enrico Fermi och Paul Dirac, är en sannolikhetsfördelning för ett stort antal identiska fermioner, med tillämpning inom främst fasta tillståndets fysik. Till skillnad från Bose–Einstein-statistik innebär Paulis uteslutningsprincip, att högst ett objekt får finnas i varje kvanttillstånd. Fördelningen kan tillämpas på exempelvis protoner, neutroner och elektroner. Fermi och Dirac härledde fördelningen oberoende av varandra 1926.^[1]

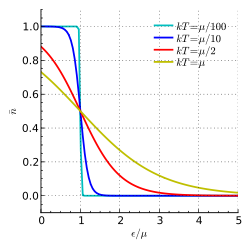
Den används främst för att beskriva elektroner i fasta kroppar tillhörande valens- och ledningsbanden, med energitillstånd som funktion av temperaturen. Sannolikheten n(ε) för att en fermion befinner sig i ett kvanttillstånd med energin ε vid temperaturen T kan tecknas

${\displaystyle n(\varepsilon )={1 \over {e^{(\varepsilon -\mu )/kT}+1}}}$

där

${\displaystyle \ \varepsilon }$   är den aktuella energinivån

${\displaystyle \ \mu }$  är den kemiska potentialen

${\displaystyle \ k}$   är Boltzmanns konstant

${\displaystyle \ T}$  är temperaturen

Vid temperaturer nära absoluta nollpunkten är för varje energinivå ${\displaystyle \ \varepsilon <\mu }$ sannolikheten nära 1 för att energinivån är besatt. Vid låga temperaturer (${\displaystyle kT\ll \mu }$) är ${\displaystyle \ \mu }$ lika med Ferminivån.

Se även

• Bose–Einstein-statistik
• Degenererad materia
• Maxwell–Boltzmannfördelning

Källor

• William Feller, An Introduction to Probability Theory and its Applications, John Wiley & Sons, New York 1950.
• Eugen Merzbacher, Quantum Mechanics, John Wiley & Sons, Toppan Company, New York 1961.
• R.E. Peierls, Quantum Theory of Solids, Clarendon Press, Oxford 1955.

Noter