Fakultet (matematik)

Den här artikeln behöver källhänvisningar för att kunna verifieras. (2020-06) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan.

Fakultet är en funktion inom matematiken. För ett heltal större än noll är fakulteten lika med produkten av alla heltal från 1 upp till och med talet självt.

Beteckning

Fakultet betecknas med ett utropstecken (!), fakultetstecken. Alltså är till exempel

${\displaystyle 3!=1\cdot 2\cdot 3=6}$

(3! utläses tre-fakultet) och allmänt för alla heltal n > 0

${\displaystyle n!=1\cdot 2\cdot 3\cdot \ldots \cdot n}$

Man gör dessutom definitionen

${\displaystyle 0!=1\ }$

På så sätt är fakultetsfunktionen definierad för alla naturliga tal.

Rekursivitet

Fakultetsfunktionen kan uttryckas rekursivt eftersom det gäller att

${\displaystyle n!=n\cdot (n-1)!}$

Rekursionen avbryts då n = 0 och 0! ≡ 1.

Till exempel är 4! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 4 ⋅ 3!

Användning inom kombinatoriken

Fakulteter förekommer mycket ofta inom kombinatoriken, bland annat när det gäller att beräkna antalet möjliga sammansättningar av ett visst antal element.

Antag till exempel att man har fyra kulor (blå, grön, gul, röd). Dessa fyra kulor kan läggas i en rad på precis 4! = 24 olika sätt (permutationer).

Detta kan förklaras såhär: När man väljer den första kulan i raden har man 4 möjliga val. När man väljer den andra kulan i raden har man 3 möjliga val (en kula är ju redan upptagen). En rad med två kulor kan alltså väljas på 4 · 3 = 12 olika sätt. Den tredje kulan kan väljas på 2 olika sätt och den fjärde på precis ett sätt. Antalet möjliga rader med fyra kulor är alltså 4 · 3 · 2 · 1 = 4! stycken.

Vidare kan man visa att antalet möjliga kombinationer av k element ur en mängd med n element är

${\displaystyle {\frac {n!}{k!(n-k)!}}}$

Här blir definitionen 0! = 1 ganska naturlig. Antalet sätt att kombinera noll element blir alltså

${\displaystyle {\frac {n!}{0!\cdot (n-0)!}}={\frac {n!}{1\cdot n!}}=1}$

Se vidare binomialkoefficient.

Generalisering

Om man definierar fakultet som en funktion som uppfyller villkoret n! = n × (n − 1)! så går det att hitta funktioner som även fungerar på mer än de naturliga talen.

Förhållandet gör att man kan beräkna fakulteten för ett heltal med hjälp av ett mindre heltal. Relationen kan inverteras så att man kan beräkna fakulteten med hjälp av ett större heltal:

${\displaystyle (n-1)!={\frac {n!}{n}}.}$

Men använder man denna formel för att beräkna (−1)! så innebär det en division med noll:

${\displaystyle {\frac {0!}{0}}.}$

Det finns två sätt att hantera detta, antingen konstruera en funktion som inte är definierad för de negativa heltalen, eller konstruera en funktion som bara uppfyller villkoret n! = n × (n − 1)! för naturliga tal.

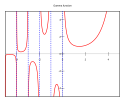
Det första sättet är den vanligaste och används i Eulers gammafunktion:

${\displaystyle \Gamma (z)=\int _{0}^{\infty }x^{z-1}e^{-x}\,dx}$

Den andra sättet är Hadamards gammafunktion:

${\displaystyle H(x)={\frac {1}{\Gamma (1-x)}}\,{\dfrac {d}{dx}}\left\{\ln \left({\frac {\Gamma ({\frac {1}{2}}-{\frac {x}{2}})}{\Gamma (1-{\frac {x}{2}})}}\right)\right\}}$

där Γ(x) står för Eulers gammafunktion^[1].

Datorberäkning

Då n är litet beräknas n! enklast genom upprepad multiplikation. Eftersom n! växer snabbt blir den här metoden dock ofta opraktisk för stora n, och i numeriska tillämpningar används i regel Stirlings formel eller liknande approximationer för att beräkna fakulteten (eller gammafunktionen) med flyttalsprecision.

Även exakta fakulteter av mycket stora heltal har många tillämpningar, exempelvis inom beräkningar som rör kombinatorik och talteori. Sådana fakulteter kan i princip beräknas genom att multiplicera alla talen 1, 2, …, n i sekvens, men detta är ineffektivt eftersom många stora delprodukter uppstår. Ett bättre angreppssätt är att rekursivt dela upp sekvensen så att delprodukterna blir mindre. Optimal prestanda uppnås genom att först bestämma alla exponenter i primtalsfaktoriseringen av n! och sedan beräkna potenserna genom upprepad kvadrering. På så sätt kan även stora binomialkoefficienter beräknas effektivt, genom att primtalsfaktorisera fakulteterna i nämnaren och täljaren och sedan subtrahera exponenter.

Faktoriseringen av n! utgörs av alla primtalen p₁, p₂ ... p_P ≤ n, där p_k har multipliciteten

${\displaystyle \sum _{i=1}^{P}\lfloor n/p_{k}^{i}\rfloor }$.

Se även

• Semifakultet
• Primorial

Källor

• Wiktionary har ett uppslag om fakultet.
  Ordbok