Faktorisering

Den här artikeln behöver källhänvisningar för att kunna verifieras. (2020-06) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan.

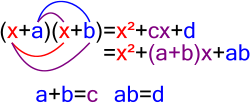
Inom matematiken innebär en faktorisering (faktoruppdelning) att man uttrycker ett objekt som en produkt av flera objekt, eller faktorer. Till exempel kan talet 15 faktoriseras i primtal som 3 ⋅ 5; och polynomet x² - 4 kan faktoriseras som (x - 2)(x + 2). Vilka sorters objekt och produkter som avses beror på sammanhanget. Exempelvis har talet 5 betraktat som naturligt tal bara den triviala faktoriseringen

${\displaystyle 5=1\cdot 5}$

uppfattat som ett vanligt heltal har det dessutom ännu en trivial faktorisering:

${\displaystyle 5=(-1)\cdot (-5)}$

men om man uppfattar 5 som ett gaussiskt heltal har det flera icke-triviala faktoriseringar, såsom

${\displaystyle 5=(1+2i)\cdot (1-2i)}$

Syftet med faktoriseringar är ofta att reducera något till "grundläggande byggstenar", såsom heltal till primtal eller polynom till irreducibla polynom.

Faktorisering i vissa fall

Tredjegradsuttryck a³ - b³ och a³ + b³ kan faktoriseras som:

${\displaystyle \ a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})}$

${\displaystyle \ a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2})}$

Primtalsfaktorisering för stora heltal verkar vara ett svårt problem. Det finns inga kända metoder för att lösa detta på kort tid. Detta är grunden för vissa kryptografiska algoritmer.

En matris kan faktoriseras till en produkt av en ortogonal matris eller unitär matris och en triangulär matris. Det finns olika typer av sådana faktoriseringar till exempel LDU, QR, LQ, QL, RQ och RZ, se matrisfaktorisering.

Se även

• Aritmetikens fundamentalsats
• Faktorsatsen