Determinant

En determinant är en funktion inom linjär algebra som tillordnar en skalär till en kvadratisk matris^[1]. Skalären anger vilka skaländringar matrisens linjära transformation ger upphov till. Geometriskt kan determinanten till exempel tolkas som den skalfaktor med vilken volymen av enhetskuben skall multipliceras för att bilda samma volym som den volym som bildas när matrisens linjära transformation tillämpas på enhetskuben. Den är även viktig inom matematisk analys, då den används vid variabelsubstitution (se jacobian).^[2]

Determinanten av en matris A betecknas det(A). Även notationen |A| används ibland men kan förväxlas med beteckningen för norm och absolutbelopp. Om alla element skall skrivas ut för determinanten används skrivsättet

${\displaystyle \det(A)={\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}}}$

En determinant av n:te ordningen

${\displaystyle {\begin{vmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\a_{2,1}&a_{2,2}&\cdots &a_{2,n}\\\vdots &&&\vdots \\a_{n,1}&a_{n,2}&\cdots &a_{n,n}\end{vmatrix}}}$

har n rader och n kolonner i ett kvadratiskt schema. Den har värdet

${\displaystyle \sum _{\sigma \in S_{n}}(\operatorname {sgn} \sigma )a_{1,\sigma _{1}}a_{2,\sigma _{2}}\cdots a_{n,\sigma _{n}}\ }$

där ${\displaystyle S_{n}\,}$ är mängden av alla permutationer av ${\displaystyle \{1...n\}\,}$. ${\displaystyle \sigma \,}$ betecknar ett element i ${\displaystyle S_{n}\,}$ och ${\displaystyle \sigma _{j}\,}$ betecknar ett element i ${\displaystyle \sigma \,}$.

Antalet termer är således ${\displaystyle n!\,}$.

Permutationer av en ordnad mängd kan åstadkommas med parvisa omkastningar av mängdens element.

Om antalet omkastningar för att åstadkomma en viss permutation är udda är tecknet för motsvarande term i summan negativt annars positivt.

Permutationerna ${\displaystyle S_{n}\,}$ av ${\displaystyle \{1,2,3\}\,}$, antalet omkastningar samt sgn-funktionens värden är

${\displaystyle {\begin{matrix}\sigma _{1}&\sigma _{2}&\sigma _{3}&&&\operatorname {sgn} \sigma \\1&2&3&:&0&+\\1&3&2&:&1&-\\2&1&3&:&1&-\\2&3&1&:&2&+\\3&1&2&:&2&+\\3&2&1&:&1&-\\\end{matrix}}}$

Determinanten för en 3×3 matris kan därmed skrivas som

${\displaystyle \ a_{1,1}a_{2,2}a_{3,3}-a_{1,1}a_{2,3}a_{3,2}-a_{1,2}a_{2,1}a_{3,3}+a_{1,2}a_{2,3}a_{3,1}+a_{1,3}a_{2,1}a_{3,2}-a_{1,3}a_{2,2}a_{3,1}}$

Varje term i summan innehåller ett element från varje kolonn och ett element från varje rad. Därmed är determinanten av en triangulär matris

${\displaystyle {\begin{vmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\0&a_{2,2}&\cdots &a_{2,n}\\\vdots &&&\vdots \\0&0&\cdots &a_{n,n}\end{vmatrix}}}$

produkten av diagonalelementen a_1,1...a_n,n.

Speciellt gäller att determinanten till enhetsmatrisen

${\displaystyle {\begin{vmatrix}1&0&\cdots &0\\0&1&\cdots &0\\\vdots &&&\vdots \\0&0&\cdots &1\end{vmatrix}}}$

har värdet 1.

Matrisen ${\displaystyle A={\begin{bmatrix}a&b\\c&d\end{bmatrix}}}$ har determinanten

${\displaystyle \det A=ad-bc\,}$

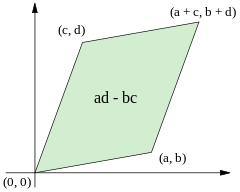
Om matrisen endast har reella element kan determinantens absolutbelopp tolkas som arean av en parallellogram med hörn i (0, 0), (a, b), (c, d) samt (a + c, b + d).

Matrisen

${\displaystyle A={\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{bmatrix}}}$

har determinanten

${\displaystyle \det A={\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}}=}$

${\displaystyle =\,a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{11}a_{23}a_{32}}$

Sarrus regel kan användas som minnesregel:

Denna regel är giltig enbart för 3×3-matriser och kan inte användas för matriser med annan storlek.

Determinantens absolutvärde kan tolkas som volymen av en parallellepiped bestämd av determinantens rader.

För en triangulär matris

${\displaystyle A={\begin{bmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\0&a_{2,2}&\cdots &a_{2,n}\\\vdots &&&\vdots \\0&0&\cdots &a_{n,n}\end{bmatrix}}}$

är determinanten lika med produkten av diagonalens element:

${\displaystyle \det A=a_{11}\cdot a_{22}\cdots a_{nn}\,}$

En matris kan trianguleras på liknande sätt som vid Gausselimination eller så kan matrisen trianguleras med hjälp av en kombination av följande regler:

1. Om två rader eller kolumner byter plats ändras det(A) till -det(A)
2. Om en rad eller kolumn multipliceras med en skalär c, ändras determinanten till c det(A)
3. Om en multipel av en rad eller kolumn adderas till en rad respektive kolumn, ändras inte determinantens värde

Laplaceutveckling överför beräkningen av en determinant till beräkning av determinanter av lägre ordning.

Om vi för en matris

${\displaystyle A={\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{bmatrix}}}$

stryker rad j och kolumn k är determinanten för återstoden av A en underdeterminant till A som hör till elementet a_jk. Om underdeterminanten betecknas D_jk får vi till exempel

${\displaystyle D_{23}={\begin{vmatrix}a_{11}&a_{12}\\a_{31}&a_{32}\end{vmatrix}}}$

Det algebraiska komplementet till a_jk definieras som

${\displaystyle A_{jk}=(-1)^{j+k}D_{jk}\,}$

Då gäller för en godtycklig matris A

${\displaystyle \det A=a_{1k}A_{1k}+a_{2k}A_{2k}+...+a_{nk}A_{nk}=\sum _{v=1}^{n}a_{vk}A_{vk},\quad k=1,2,...,n}$

vilket kallas utveckling av determinanten efter kolumn k. Motsvarande för utveckling efter rad j är

${\displaystyle \det A=a_{j1}A_{j1}+a_{j2}A_{j2}+...+a_{jn}A_{jn}=\sum _{v=1}^{n}a_{jv}A_{jv},\quad j=1,2,...,n}$

Exempel på Laplaceutveckling av en tredje ordningens determinant efter kolumn 1:

${\displaystyle {\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}}=a_{11}{\begin{vmatrix}a_{22}&a_{23}\\a_{32}&a_{33}\\\end{vmatrix}}-a_{21}{\begin{vmatrix}a_{12}&a_{13}\\a_{32}&a_{33}\\\end{vmatrix}}+a_{31}{\begin{vmatrix}a_{12}&a_{13}\\a_{22}&a_{23}\\\end{vmatrix}}}$

Gausselimineringsliknande metod

Vid Gausseliminering sker division med elementen i diagonalen. Utgående från aktuell kolonns diagonalelement, är pivotelementet det element som har det största absolutbeloppet av de återstående elementen i kolonnen. Genom radomkastningar placeras pivotelementet i diagonalen och därigenom minskas risken att dividera med tal som är nära noll. Om inget nollskilt pivotelement hittas avbryts elimineringen och determinanten tilldelas värdet 0. Beräkna determinanten till matrisen ${\displaystyle A={\begin{bmatrix}1&2&3\\1&6&8\\2&8&17\end{bmatrix}}}$ genom att först triangulera matrisen. 1 Med början i element A(1,1), sök det tal, pivotelementet, som har det största absolutbeloppet i kolonn 1. A(3,1) väljs som pivotelement. Nollställ radomkastningsräknaren n. 2 Låt rad 1 och pivotelementets rad byta plats. Addera 1 till radomkastningsräknaren n. 3 Nollställning av element A(2,1): multiplicera en kopia av rad 1 med -A(2,1)/A(1,1) och addera resultatet till rad 2. Nollställning av element A(3,1): multiplicera en kopia av rad 1 med -A(3,1)/A(1,1) och addera resultatet till rad 3. 4 Sök pivotelementet med början i nästa diagonala element, A(2,2). A(2,2) väljs som pivot. 5 Då aktuell rad också är pivotelementets rad sker ingen radomkastning. Nollställning av element A(3,2): multiplicera en kopia av rad 2 med -A(3,2)/A(2,2) och addera resultatet till rad 3. 6 Matrisen är triangulerad. Determinanten beräknas som produkten av diagonalelementen. Om radomkastningsräknarens värde är udda tillkommer en faktor -1: ${\displaystyle \det(A)=(-1)^{n}\cdot 2\cdot 2\cdot (-6)=24}$

• ${\displaystyle \det(AB)=\det(A)\det(B)\,}$ för alla n×n-matriser A och B.

• ${\displaystyle \det(rA)=r^{n}\det(A)\,}$ för alla n×n-matriser A och alla skalärer r.

• ${\displaystyle \det(A^{-1})=\det(A)^{-1}\,}$

• Matrisen och dess transponat har samma determinant:

${\displaystyle \det(A^{\top })=\det(A)\,}$.

• Determinanten är invariant under basbyte. Om en matris A kan representas som matris B, det vill säga ${\displaystyle A=TBT^{-1}}$, så gäller:

${\displaystyle \det(A)=\det(TBT^{-1})=\det(T)\det(B)\det(T^{-1})=\det(T)\det(T)^{-1}\det(B)=\det(B)\,}$

• Determinanten är produkten av matrisens egenvärden, det vill säga om A har egenvärdena ${\displaystyle \lambda _{1},...,\lambda _{n}}$ är

${\displaystyle \det(A)=\lambda _{1}\cdots \lambda _{n}\,}$

vilket trivialt gäller för diagonaliserbara matriser. För icke diagonaliserbara matriser kan man använda Schurs sats och få en triangulär matris genom att steg för steg utveckla efter första kolumnen.

Determinanter används för att karakterisera matriser och att explicit beskriva lösningar av dess motsvarande linjära ekvationssystem.

Om determinanten för ett homogent ekvationssystem är noll finns icke-triviala lösningar, för övriga värden på determinanten är den enda lösningen den triviala lösningen.

I ett inhomogent system där determinanten är noll finns ingen eller oändligt antal lösningar. Är determinanten nollskild har ekvationssystemet en unik lösning.

Determinanten kan även användas för att hitta egenvärdena för en matris ${\displaystyle A}$ via sekularekvationen ${\displaystyle \det(A-\lambda I_{n})=0}$.

Determinanter uppstod av problem kring linjära ekvationssystem,

${\displaystyle {\begin{matrix}a_{1}x_{1}+a_{2}x_{2}+a_{3}x_{3}=0\\b_{1}x_{1}+b_{2}x_{2}+b_{3}x_{3}=0\\c_{1}x_{1}+c_{2}x_{2}+c_{3}x_{3}=0\end{matrix}},}$

nämligen att hitta icke-triviala lösningar (x₁ ≠ 0, x₂ ≠ 0, x₃ ≠ 0) och under vilka förutsättningar dessa går att finna. (Jämför Cramers regel)

Med a = (a₁, a₂, a₃), b = (b₁, b₂, b₃), c = (c₁, c₂, c₃) och x = (x₁, x₂, x₃), kan ovanstående ekvationssystem skrivas med vektornotation enligt

${\displaystyle {\begin{matrix}\mathbf {a} \cdot \mathbf {x} =0\\\mathbf {b} \cdot \mathbf {x} =0\\\mathbf {c} \cdot \mathbf {x} =0\\\end{matrix}}}$

Den geometriska tolkningen av ovanstående tre skalärprodukter är att x är ortogonal till samtliga vektorer a, b och c. Om volymen som spänns upp av dessa koefficientvektorer, det vill säga om trippelprodukten eller determinanten av vektorerna a, b och c

${\displaystyle (\mathbf {a} \times \mathbf {b} )\cdot \mathbf {c} =\det(\mathbf {a} ,\mathbf {b} ,\mathbf {c} )={\begin{vmatrix}a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\c_{1}&c_{2}&c_{3}\end{vmatrix}}}$

inte är noll, finns endast den triviala lösningen x = 0.

Om så inte är fallet är någon av koefficientvektorerna en linjärkombination av de övriga två. Säg att c är en linjärkombination av a och b. Detta innebär att x ∝ a×b vilket ger x·c = 0. I detta fall finns oändligt många lösningar av ekvationssystemet.

Determinater beräknades innan begreppet "matris" fanns och betraktades då som en egenskap hos linjära ekvationssystem, eftersom determinanten avgör (latin: determino) om systemet har en unik lösning. Determinanter för 2×2-matriser studerades av Gerolamo Cardano under 1500-talet, men begreppet introducerades århundradet efter av Gottfried Leibniz, som även studerade determinanter för större system. 1750 utvecklade Gabriel Cramer teorin.

Alexandre-Théophile Vandermonde (1771) insåg att determinanten hade tillämpningar utanför ekvationssystemen. 1772 presenterade Pierre Simon de Laplace sin metod för expansion i underdeterminanter. Vandermonde hade då redan gett ett specialfall. Redan 1773 behandlade sedan Joseph Louis Lagrange andra och tredje ordningens determinanter och han var även den förste att använda determinanter i andra sammanhang än elimination samt lyckades visa flera specialfall av generella samband.

År 1801 utvidgade Carl Friedrich Gauss området. På samma sätt som Lagrange använde han ofta determinanterna inom talteori och var den förste att använda ordet determinant (Laplace hade använt resultant), även om det inte var i den nuvarande meningen.

Nästa betydande bidrag gavs av Jacques Philippe Marie Binet, som 1811 och 1812 formellt gav resultatet om determinanten för produkten av två n × m-matriser (Cauchy-Binets formel), som för specialfallet n=m reduceras till multiplikationssatsen enligt ovan. Den 30 november 1812, när han presenterade sina resultat för akademin presenterade även Augustin Louis Cauchy vad han kommit fram till i ämnet. Han blev då den förste att använda ordet determinant i sin moderna betydelse och lyckades summera och förenkla vad som var känt inom ämnet och gav ett bättre bevis än det Binet presenterade.

1827 blev sedan Carl Gustav Jakob Jacobi näste viktige bidragsgivare, genom att använda den funktional-determinant som senare skulle bli känd under namnet Jacobian.

• Kryssprodukt
• Seki Shinsuke Kowa

• Wikimedia Commons har media som rör Determinant.
  Bilder & media

Linjär algebra Grundläggande begrepp Skalär · Vektor · Noll · Ortogonalitet · Ekvationssystem · Rum · Linjärkombination · Inre produkt · Oberoende · Bas · Radrum · Kolonnrum · Nollrum · Gram-Schimdt · Egenvärde · Hölje · Linjäritet Vektoralgebra Kryssprodukt · Trippelprodukt Matriser Elementär · Block · Enhet · Determinant · Norm · Rang · Transformation · Rotation · Invers · Cramers regel · Trappstegsform · Spår · Transponat · Gausselimination · Symmetri · Addition Multilinjär algebra Geometrisk algebra · Yttre algebra · Bivektor · Multivektor · Tensor Konstruktioner Delrum · Dualrum · Funktionsrum · Kvotrum · Tensorprodukt Numerik Flyttal · Gles matris Kategori