Dedekinds etafunktion

Inom matematiken är Dedekinds etafunktion, uppkallad efter Richard Dedekind, en viss modulär form av vikt 1/2. För komplexa tal τ med positiv imaginär del låtq = exp(2πiτ). Då definieras Dedekinds etafunktion som
Etafunktionen är analytisk i övre planhalvan men kan inte fortsättas analytiskt utanför den.

Etafunktionen satisfierar funktionalekvationerna
Mer generellt, antag att a, b, c, d är heltal med ad − bc = 1, sådana att
är en transformation i modulära gruppen. Vi kan anta att antingen c > 0 eller c = 0 och d = 1. Då är
där
Här betecknar Dedekindsumman
Speciella värden
Se även
- Chowla–Selbergs formel
- Weierstrass elliptiska funktion
- Heltalspartition
- Supersträngteori
Referenser
- Den här artikeln är helt eller delvis baserad på material från engelskspråkiga Wikipedia, Dedekind eta function, 7 mars 2014.
Källor
- Tom M. Apostol, Modular functions and Dirichlet Series in Number Theory (2 ed), Graduate Texts in Mathematics 41 (1990), Springer-Verlag, ISBN 3-540-97127-0 Se kapitel 3.
- Neil Koblitz, Introduction to Elliptic Curves and Modular Forms (2 ed), Graduate Texts in Mathematics 97 (1993), Springer-Verlag, ISBN 3-540-97966-2
Media som används på denna webbplats
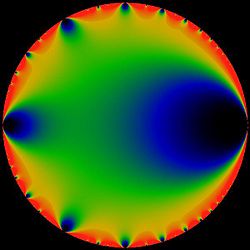
function DedekindEta[z] in the complex plane
(c) Linas from en.wikipedia.org, CC BY-SA 3.0
This picture shows the modulus on the complex plane, inside the unit circle , where
is Euler's q-series for the Partition of an integer. The fractal self-similarity of this function is that of the modular group; note that this function is closely related to a modular form, the modular discriminant. Every modular function will have this general kind of self-similarity.
It is colored with a rainbow of colors, with black representing values near zero, and red values near four. Note the Modular group symmetry, and the
general resemblance to colorings of the interior of the Mandelbrot set.