Snells lag

Den här artikeln behöver källhänvisningar för att kunna verifieras. (2017-03) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan.

Snells lag, även känd som brytningslagen ^[1] eller allmänna brytningslagen^[2], är formeln som används för att beräkna vinklarna vid refraktion (ljusbrytning) då ljus färdas mellan två medier med olika brytningsindex. Den är uppkallad efter dess holländske upptäckare Willebrord Snell (1580–1626).

Sammanfattning

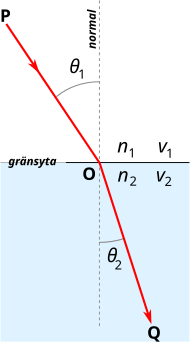
I diagrammet till höger möts två medier med brytningsindexen n₁ (till vänster) och n₂ (till höger) i en gemensam gränsyta (den vertikala linjen). Brytningsindexet för det andra mediet är högre än brytningsindexet för det första mediet (n₂ > n₁), vilket gör att ljuset har en mindre fashastighet inuti det andra mediet.

En ljusstråle PO i det vänstra mediet infaller mot gränsytan i punkten O- I punkten O introducerar vi en till gränsytan rätvinklig linje (gränsytans normal). Vinkeln mellan normalen och ljusstrålen PO kallas infallsvinkeln θ₁.

Ljusstrålen fortsätter genom gränsytan in i mediet till höger, linjen OQ. Dess vinkel till normalen bildar brytningsvinkeln θ₂.

Snells lag ger relationen mellan vinklarna θ₁ och θ₂.

${\displaystyle n_{1}\sin(\theta _{1})=n_{2}\sin(\theta _{2}).\,}$

Då θ₁ = 0° (det vill säga då ljusstrålen träffar gränsytan i rät vinkel) är lösningen alltid θ₂ = 0° oavsett värdena på n₁ och n₂. Det betyder med andra ord att en ljusstråle som träffar gränsytan i rät vinkel aldrig bryts.

Detta samband gäller också då ljus färdas från ett tätare medium till ett tunnare - symmetrin i Snells lag ger att samma strålbanor kan tillämpas i motsatt riktning.

En bra minnesregel för att bestämma ljusbrytningens riktning är det faktum att ljusstrålen i det tätare mediet alltid befinner sig närmare normalen. Ett praktiskt sätt att komma ihåg detta är att tänka sig ljusstrålen som en bil som kör från en asfalterad yta (det tunnare mediet) och in på lerigt underlag (det tätare mediet). Beroende på vinkeln kommer då antingen det högra eller det vänstra hjulet att passera gränsen först vilket gör att bilen svänger.

Totalreflektion

När en ljusstråle färdas från ett tätare medium till ett tunnare (det vill säga n₁ > n₂) kan man lätt konstatera att ekvationen saknar lösning då θ₁ överstiger ett visst kritiskt värde kallat gränsvinkeln θ_g. Detta beroende på att sin(θ₁) alltid är mindre än (eller lika med) 1.

${\displaystyle \theta _{g}=\arcsin \left({\frac {n_{2}}{n_{1}}}\right)}$

Då θ₁ > θ_g lyckas inget ljus passera gränsytan och totalreflexion inträffar vilket innebär att allt infallande ljus återspeglas. Detta kan till exempel inträffa när ljus färdas genom vatten till luft eftersom vatten är ett optiskt tätare medium än luft (n_vatten > n_luft), om infallsvinkeln samtidigt överstiger θ_g.

Vektorform

Givet en vektor v av längd 1 (enhetsvektor) som ger ljusets riktning, och en enhetsvektor p vinkelrät mot gränsytan, så kan generaliserade reflexions- och brytningsvinklar beräknas. Generaliseringen innebär att de faktiska vinklarna θ₁ och θ₂ inte beräknas.

${\displaystyle \cos \theta _{1}=\mathbf {v} \cdot \mathbf {p} }$

${\displaystyle \cos \theta _{2}={\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\right)^{2}\left(1-\left(\cos \theta _{1}\right)^{2}\right)}}}$

${\displaystyle \mathbf {v} _{\mathrm {reflexion} }=\mathbf {v} -\left(2\cos \theta _{1}\right)\mathbf {p} }$

${\displaystyle \mathbf {v} _{\mathrm {brytning} }=\left({\frac {n_{1}}{n_{2}}}\right)\mathbf {v} +\left(\cos \theta _{2}-{\frac {n_{1}}{n_{2}}}\cos \theta _{1}\right)\mathbf {p} }$

Cosinustermerna kan återanvändas i Fresnelekvationerna för att beräkna de resulterande ljusstrålarnas intensitet. Rotutdragningarna leder till imaginära tal vid totalreflexion, och ljusstrålen som bryts är inte reell. Man kan då betrakta den brutna strålen som att den avtar exponentiellt, mycket snabbt med avståndet från ytan.

Härledning

Snells lag kan härledas från Fermats princip som säger att ljuset tar den väg som tar minst tid. Genom att bilda den optiska banlängdens derivata, kan den stationära punkt som ljuset passerar hittas. I Richard Feynmans klassiska analogi har det lägre brytningsindexet ersatts av en strand och det högre indexet av havet. Den snabbaste vägen för en badvakt på stranden att nå en drunknande människa är att följa den väg som utpekas av Snells lag.

Historia

Förmodligen upptäcktes Snells lag först av Ibn Sahl på 900-talet som använde den för att beräkna den optimala formen på linser. Den återupptäcktes av Thomas Harriot i slutet av 1500-talet. Under 1600-talet upptäcktes sambandet på nytt av Willebrord Snell och René Descartes oberoende av varandra. Attributionen dem emellan är inte helt tydlig och i Frankrike kallas Snells lag fortfarande för "la loi de Descartes".

Se även

• Fermats princip
• Refraktion
• Reflexion (fysik)

Referenser

Externa länkar

• (engelska) Om upptäckten av allmänna brytningslagen