Binärsökning

Binärsökning
Sökalgoritm, söndra-och-härska-algoritm
Binärsökningsträd med 9 noder och höjden 4.

Binärsökning är en algoritm för att avgöra om en mängd innehåller ett givet element. Sökningen utförs i flera steg och i varje steg skall man utesluta att halva den kvarvarande mängden innehåller elementet och därmed kunna koncentrera sig på den andra halvan.

Intervallhalveringsmetoden är en term som används om både binärsökning och den matematiska problemlösningsmetoden i Bolzanos sats.

Ett exempel på binärsökning är uppslagning av ett ord eller namn i en alfabetiskt ordnad lista, till exempel en tryckt telefonkatalog eller en ordbok. Man börjar med att titta i mitten av listan. Genom att jämföra det sökta ordet med det som står i mitten av listan, vet man vilken halva av listan man ska fortsätta med. Efter andra uppslagningen återstår bara en fjärdedel av listan.

Om hela listan har N uppslagsord, krävs högst uppslagningar eller halveringar för att hitta rätt ställe, eller 2-logaritmen avrundad uppåt.

Antal noder
2-logaritmen
avrundad uppåt
Kommentar
93,174Grafen i bilden här intill har 9 noder och höjden 4.
9009,8110
1 953 03320.821Alla artiklar i svenskspråkiga Wikipedia (januari 2015).
9 miljoner23,124En katalog över hela Sveriges befolkning.
6 miljarder32,533En katalog över hela jordens befolkning.

Ett sätt att illustrera sökningen är som ett binärt sökträd där varje nod i trädet har maximalt två barn det ena måste vara större än och det andra mindre än nodens egna element. Alla noder i trädet är element i listan. Trädets höjd är högsta antalet uppslagningar som sökningen kräver.

Algoritm

Binärsökning söker igenom sorterade listor. Binärsökning börjar med att jämföra elementet i mitten av listan med det sökta värdet. Om det sökta värdet är lika med elementet i mitten av listan, returneras dess position i listan. Om det sökta värdet är mindre eller större än elementet i mitten av listan, så fortsätter sökningen i den lägre respektive högre halvan av listan, rekursivt.

Procedur

Följande samling av instruktioner utgör en binärsökningsalgoritm för att hitta positionen av värdet T i listan A, som innehåller n element med värdena A0 , A1, ..., An-1.

  1. Sätt L till 0 och R till n − 1.
  2. Om L > R, så har binärsökningen misslyckats.
  3. Sätt m (positionen av elementet i mitten av listan) till heltalsdelen av (L + R) / 2.
  4. Om Am < T, sätt L till m + 1 och gå till steg 2.
  5. Om Am > T, sätt R till m − 1 och gå till steg 2.
  6. Nu är Am = T, sökningen är färdig; returnera m.

Den iterativa proceduren håller reda på sökområdet med de två variablerna (L och R).

Media som används på denna webbplats

Arbcom ru editing.svg
Icon of simple gray pencil. An icon for Russian Wikipedia RFAR page.
Binary Search Depiction.svg
Författare/Upphovsman: AlwaysAngry, Licens: CC BY-SA 4.0
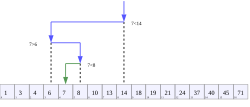
This is an example of a binary search steps through time. Source code and output: 
int[] numbersArray = {1,3,4,6,7,8,10,13,14,18,19,21,24,37,40,45,71};
public boolean binarySearchAlgorithm(int targetNumber, int[] numbers)
{
    int lowerLimit = 0;
    int upperLimit = numbers.length - 1;

    while (upperLimit >= lowerLimit)
    {
        int middleNumber = (lowerLimit + upperLimit)/2;

        if (numbers[middleNumber] == targetNumber)
        {
            return true;
        }
        if (numbers[middleNumber] < targetNumber)
        {
            lowerLimit = middleNumber + 1;
        }
        if (numbers[middleNumber] > targetNumber)
        {
            upperLimit = middleNumber - 1;
        }
    }
    return false;
}
System.out.println(binarySearchAlgorithm(7, numbersArray)); //prints "true"

iteration 1

  1. low = 0
  2. high = 16
  3. middle = (0+16)/2 = 16/2 = 8
  4. 7 (target at index 4) < 14 (middle at index 8)
  5. high = middle - 1 = 7

iteration 2

  1. low = 0
  2. high = 7
  3. middle = (0+7)/2 = 7/2 = 3 R 1
  4. 7 (target at index 4) > 6 (middle at index 3)
  5. low = middle + 1 = 4

iteration 3

  1. low = 4
  2. high = 7
  3. middle = (4+7)/2 = 11/2 = 5 R 1
  4. 7 (target at index 4) < 8 (middle at index 5)
  5. high = middle - 1 = 4

iteration 4

  1. low = 4
  2. high = 4
  3. middle = (4+4)/2 = 8/2 = 4
  4. 7 (target at index 4) == 7 (middle at index 4)
Binary search tree.svg

Created by Derrick Coetzee in Adobe Illustrator. This SVG, based on the original .ai file, supplants the PNG Image:Binary_search_tree.png.