Anslutningsmatris
En anslutningsmatris (eller incidensmatris) är inom matematik, specifikt grafteori, en matris som beskriver vilka noder i en graf bågarna är kopplade till. Inom projektiv geometri beskriver den vilka punkter som är incidenta med vilka linjer.
Även grannmatriser är matriser som beskriver grafer.
Definition
Inom grafteori finns flera olika anslutningsmatriser, en typ som bara kan användas på oriktade grafer och en som används för riktade grafer och kan anpassas till oriktade grafer.
Oriktad anslutningsmatris
För en oriktad graf G med nodmängd och bågmängd så är den oriktade anslutningsmatrisen A en matris av storlek n × b där elementet om noden är kopplad till bågen och noll annars.
Riktad anslutningsmatris
Den riktade anslutningsmatrisen A för en riktad graf G med noder och riktade bågar som ovan, är n × b-matrisen med elementen som är 1 om bågen går till noden , -1 om bågen går från och 0 annars.
För riktade grafer kan man definiera en riktad anslutningsmatris helt enkelt genom att välja en riktning för alla bågar i grafen. En oriktad graf har alltså flera riktade anslutningsmatriser.
Hypergrafer
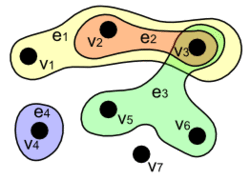
I en vanlig graf kan en båge endast vara ansluten till två noder, så i varje kolonn i en anslutningsmatris kan det bara finnas två nollskilda element. I en hypergraf kan en båge vara ansluten till flera noder, så att en kolonn kan ha flera nollskilda element i sin oriktade anslutningsmatris.
Exempel
Anslutningsmatriser kan läsas kolonnvis då man läser vilka noder som är direkt anslutna med en båge, eller radvis, då man läser vilka bågar som är ansluten till en specifik nod.
| Graf/hypergraf | Oriktad anslutningsmatris | Riktad anslutningsmatris |
|---|---|---|
 | ||
 | Ej tillämpbart. | |
 | Ej tillämpbart. |
Egenskaper
Om G är en oriktad graf med oriktad anslutningsmatris A och linjegraf L så är , där är grannmatrisen till L.
Den riktade anslutningsmatrisen till en riktad graf är fullständigt unimodulär.
Referenser
- Godsil, Chris; Gordon Royle (2001). Algebraic Graph Theory. Springer Verlag. ISBN 0-387-95241-1
- Lundgren, Jan; Peter Värbrand, Mikael Rönnqvist (2008). Optimeringslära. Studentlitteratur. ISBN 9789144053141
Media som används på denna webbplats
Labeled, undirected graph with four edges and four vertices.
Författare/Upphovsman: Calle, Licens: CC BY-SA 3.0
Riktad graf med numrerade bågar. Gjort i Openoffice Draw.