Alternerande grupp

En alternerande grupp är en grupp bestående av de jämna permutationerna av en ändlig mängd. Den alternerande gruppen av mängden {1,...,n}, kallas för den alternerande gruppen av grad n och betecknas med A_n eller Alt(n). A_n är en normal delgrupp till den symmetriska gruppen S_n och antalet element är lika med n!/2.

Den alternerande gruppen A_n är definierad för n ≥ 2. Om och endast om n = 2 eller n = 3, är A_n abelsk. A₄ är den enda alternerande gruppen, som inte är enkel, det vill säga A₄ har en icke-trivial normal delgrupp, Kleins fyrgrupp. För n ≥ 5 har A_n således endast triviala normaldelare.

(c) Debivort, CC-BY-SA-3.0

Cykelgraf, som visar de tolv rotationerna av en tetraeder. Blå pilar är 180- och röda pilar 120-graders vridningar.

Exempel

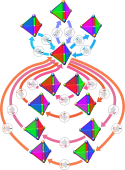
I en tetraeder med hörnen numrerade 1, 2, 3 och 4 är A₄ den grupp, som beskriver kroppens 12 möjliga vridningar: Två vridningar om 120 grader runt var och en av tetraederns fyra höjder, en vridning om 180 grader runt vardera av de tre axlar, som sammanbinder mittpunkterna på två motstående sidokanter samt ingen vridning alls. Totala antalet vridningar = 4·2 + 3·1 + 1 = 12. Med cykler kan gruppen skrivas {(123), (132), (124), (142), (134), (143), (234), (243), (12)(34), (13)(24), (14)(23), e}. Gruppens cykelstruktur kan skrivas som 8x₁x₃ + 3x₂² + x₁⁴

A₄ har fem icke-triviala delgrupper, en 2-sylowgrupp som är unik och därför, som en följd av Sylows tredje sats, normal och fyra 3-sylowgrupper. A₄ är den minsta grupp för vilken kan visas, att omvändningen till Lagranges sats inte gäller. Gruppen har, trots att dess ordning är delbar med 6, inte någon delgrupp av ordning 6.

Källor

• I. N. Herstein, Topics in Algebra, Blaisdell Publishing Company, Waltham 1964.
• B. L. van der Waerden, Algebra, Springer-Verlag, Heidelberg 1950.
• Karl-Johan Bäckström, Diskret matematik, Studentlitteratur, Lund 1986.

S₄ och A₄

Cayleytabell av symmetriska gruppen S₄. De udda permutationerna är färgade. Transpositionerna är gröna och 4-cyklerna är orange.

Cayleytabell av alternerande gruppen A₄. Elementen är de jämna permutationerna: Identiteten, åtta 3-cykler och tre dubbeltranspositioner.