Åttahörning
 |  | |
Stopp-skylten har en regelbundet åttahörnig form. | Paraplyer sedda uppifrån. |
En åttahörning, åtthörning, oktogon eller oktagon, eller någon gång åttkant, är en polygon som består av åtta (räta) linjestycken, som bildar en enkel sluten kurva.[1]Ofta har man med oktogon eller oktagon menat en regelbunden åttahörning[2], det vill säga en liksidig och likvinklig åttahörning (med alla sidor respektive vinklar lika stora). Summan av (de inre) vinklarna i en åttahörning är alltid 1080° (6π). En regelbunden åttahörning har därför vinkeln ; den har Schläfli-symbolen .
I Sverige och flera andra länder har stoppskyltar, det vill säga skyltar som visar att stopplikt gäller, formen av en regelbunden åttahörning.
Regelbundna åttahörningar

För en regelbunden åttahörning med sidlängden gäller (se figur 2):
Area
En regelbunden åttahörning har arean:
- Härledning
- En regelbunden åttahörning är en kvadrat med fyra avskurna hörn (som i figur 3). Dessa hörn är rätvinkliga trianglar med hypotenusan och de liklånga kateterna är sålunda [3] vilket ger att den hela kvadraten har sidlängden och därmed arean . De fyra bortskurna trianglana har sammanlagt arean [4] vilket subtraheras från kvadraten och ger resten .
Diagonaler

Diagonalerna (figur 2) har längderna:
- Härledning
- Längden för visades ovan under Area vara
- Betrakta den rätvinkliga triangeln i figur 2 vars hypotenusa har längden och vars kateter har längderna och . Pythagoras sats ger
- Betrakta en rätvinklig triangel där (ej utmärkt i figur 2 men ligger i skärningspunkten mellan r1 och d2) är fotpunkt till på . Dess hypotenusa har längden och, eftersom är en likbent rätvinklig triangel med hypotenusan och följdakligen båda kateterna [3] , har kateterna i längderna respektive .
- Pythagoras sats ger:
De inskrivna och omskrivna cirklarna
Radierna fås direkt genom halvering av de två av diagonalerna som är liklånga med cirklarnas respektive diametrar:
Den inskrivna cirkelns radie är
Den omskrivna cirkelns radie är
Cirklarnas omkretser och areor fås därefter givetvis av respektive .
"Silversnittet" och "cordobasnittet"

De om- och inskrivna cirklarnas radier och diametrar eller, om man så vill, diagonalerna och , anses ha spelat roll inom arkitektur och konst, där kvoten mellan dessa och åttahörningens sidlängd stundom använts. "Cordobasnittet" (engelska Cordovan ratio, uppkallad efter proportioner hos byggnader, särskilt stora moskén, i Cordoba, Spanien) är kvoten mellan den omskrivna cirkelns radie och åttahörningens sidlängd, vilka tillsammans bildar sidorna i "cordobatrianglen" (Cordovan triangle), medan cirkelns diameter och sida bildar sidorna i "cordobarektangeln" (Cordovan rectangle med proportionerna ). Kvoten mellan den inskrivna cirkelns diameter och åttahörningens sidlängd, , har sedan ungefär senaste milleniumskifte ibland kallats "silversnittet" (på engelska silver ratio[5]), eller det "silverne snittet", i analogi med det "gyllene snittet" (som är förhållandet mellan sidlängd och diagonal i en regelbunden femhörning). Likaledes kallas ibland en rektangel med denna proportion mellan sidorna en "silverrekttangeln" (silver rectangle).[6][7] "Silversnittet" betecknas eller . Ett papper av A-format (exempelvis ett vanligt A4-papper) kan delas i en kvadrat och en "silverrektangel"[8] eftersom ett sådant papper har proportionerna och tar man bort en kvadrat med sidlängden 1 från detta har den återstående remsan proportionerna .[9][10]
Konstruktion från en kvadrat

Hur man viker en regelbunden åttahörning utgående från ett kvadratiskt papper framgår av figuren till höger, men är materialet "styvare" får man ta till andra sätt, som passare och linjal (samma princip som pappersvikningen: dra diagonalerna med linjal, mät ut kvadratens sida med passaren på diagonalen och konstruera mittpunktsnormalen till den återstående biten av diagonalen) eller direkt mätning:
Se figur 3. Eftersom kateterna på de gröna rätvinkliga trianglar som skall "skäras bort" från kvadraten har längden och hela kvadraten har sidlängden (se ovan under Diagonaler) i förhållande till den önskade åttahörningens sidlängd , har vi att kateterna på de trianglar som skall skäras bort har längden:
- .
- I praktiken
- Multiplicera din spånskivekvadrats sidlängd med 0,293 och märk ut punkter på kvadratens sidor med detta avstånd från hörnen. Dra räta linjer mellan punkterna och följ linjerna när du sågar. Om du vill ha en regelbunden åttahörning med en bestämd sidlängd utgår du från en kvadrat med sidor som är gånger så långa som denna önskade längd.
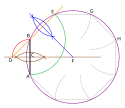
Konstruktion från en given sida med passare och linjal

Givet sidan [12] (svart) i figuren till höger.
Dra mittpunktsnormalen (brun konstruktion) till och kalla sidans mittpunkt . Placera passaren i och avsätt på mittpunktsnormalen (symboliserat av röd cirkelbåge) och kalla denna punkt . Dra den räta linjen genom och (orange).[13] Sätt passaren i och avsätt på den nyss dragna (orange) linjen genom och (symboliserat av grön cirkelbåge) och kalla denna punkt . Vi har nu fått sidan ! Konstruera mittpunktsnormalen (blå konstruktion) till . De två mittpunktsnormalerna (till respektive ) skär varandra i , oktoederns mittpunkt och den omskrivna cirkelns mittpunkt. Placera passaren i och rita den omskrivna cirkeln (violett) med radien . Avsätt sedan runt denna cirkel hörn för hörn (symboliserat av streckade linjer).
Etymologi för de grecistiska namnen
Namnen oktogon och oktagon kommer från senlatinets oc'togonum/oc'tagonon Dit har ordet hämtats från det grekiska adjektivet Οκτάγωνος ok'tagōnos (av ὀκτώ oktōʹ 'åtta' och -γωνος -gō'nos 'vinklig'). I båda språken har ordet betydelsen 'åttahörning'. Begreppet stavas i olika europeiska språk antingen med centralt -a- (i analogi med oktaeder och andra lånord från grekiskan) eller -o- (i analogi med oktober och andra latinska bildningar baserade på grekiska lånord). I svenska språket förekommer båda varianterna, även om oktogon-stavningen i mitten av 1900-talet var den vanligaste.[14][15][16]
Referenser och noter
- ^ ”oktogon”. ne.se. https://www.ne.se/uppslagsverk/encyklopedi/l%C3%A5ng/oktogon. Läst 24 juli 2018.
- ^ ”OKTOGON”. Svenska Akademiens ordbok. https://svenska.se/saob/?id=O_0283-0220.u4Zq&pz=7.
- ^ [a b] Enligt Pythagoras sats: .
- ^ fyra trianglar, vardera med en area som är halva produkten av bas=katet och höjd=katet
- ^ Även det inverterade gyllene snittet kallas "silver ratio". Se Eric Wesstein, Golden ratio conjugate på Wolfram MathWorld.
- ^ Antonia Redondo Buitrago & Encarnación Reyes Iglesias, Geometry and Art from the Cordovan Proportion och The Geometry of the Cordovan Polygons.
- ^ Tomas Gil-Lopez, 2012, The Vault of the Chapel of the Presentation in Burgos Cathedral: "Divine Canon? No, Cordovan Proportion", Nexus Network Journal, 14:1.
- ^ Inom origami-kretsar kallas dock själva A-formatet för silver rectangle. Se David Lister The A4 rectangle Arkiverad 18 oktober 2018 hämtat från the Wayback Machine. på British Origami Society.
- ^
- ^ Hemmapysslaren kan sålunda enkelt av ett A4-papper framställa en "silverrektangel" med måtten 210×87 mm och, med hjälp av denna som mall , tillverka en regelbunden åttahörning med sidlängden 87 mm av den återstående kvadraten (vik rektangeln längs med på mitten, vik ut den igen och lägg vecket längs kvadratens diagonaler).
- ^ Förläng med i näst sista steget.
- ^ betecknar sträckan mellan punkterna och , betecknar längden av sträckan .
- ^ Eftersom och vinkeln i är rät bildar vinkeln 45° mot på åttahörningens utsida och därför vinkeln 180° - 45° = 135° på dess insida.
- ^ Oktogon i SAOB.
- ^ Octagon i Merriam-Webster.
- ^ Octagon Arkiverad 14 augusti 2019 hämtat från the Wayback Machine. i Oxford Dictionaries.
| |||||||||||
Media som används på denna webbplats
Författare/Upphovsman: Episcophagus, Licens: CC BY-SA 4.0
The silver rectangle in an octagon.
Författare/Upphovsman: Episcophagus, Licens: CC BY-SA 4.0
How to construct a regular octagon with ruler and compass feom a given side.
Författare/Upphovsman: Raoul NK, Licens: CC BY-SA 4.0
Building the octagon via folding of paper
An octagon of side length a in a circle of side length S, where S is the span of the octagon. The area of the octagon, A, is then given by
- .
Författare/Upphovsman: Toni Castillo Quero, Licens: CC BY-SA 2.0
The Mezquita of Córdoba seen from the air (Córdoba, Spain)